Question

如图，在矩形ABCD中，O是AC与BD的交点，过O点的直线EF与AB、CD的延长线分别交于点E、F，连接AF、EC． (1)证明：△BOE≌△DOF． (2)当EF与AC满足什么条件时，四边形AECF是菱形？为什么？

Answer 1

答案：
解析：

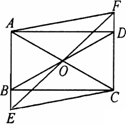
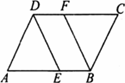
(1)证明：因为四边形ABCD是矩形，所以AB∥CD，BO＝OD，所以∠BEO＝∠DFO，∠EBO＝∠FDO，所以△BOE≌△DOF． 　　(2)解：当EF与AC垂直时，四边形AECF是菱形．理由如下： 　　因为△BOE≌△DOF，所以EO＝FO． 　　又因为矩形ABCD中，AO＝OC，所以四边形AECF为平行四边形． 　　又因为EF⊥AC，所以四边形AECF是菱形．