题目内容
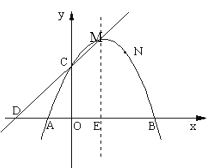
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数![]() 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.
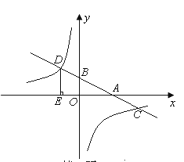
(1)求反比例函数与一次函数的解析式.
(2)根据图象写出不等式kx+b>![]() 的解集.
的解集.
(3)连接OC、OD,求![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)x<-2或0<x<6;(3)面积为8
;(2)x<-2或0<x<6;(3)面积为8
【解析】
(1)将C坐标代入反比例解析式中求出m的值,确定出反比例解析式,再由DE为3得到D纵坐标为3,将y=3代入反比例解析式中求出x的值,即为D的横坐标,将D与C的坐标代入y=kx+b求出k与b的值,即可确定出一次函数解析式;
(2)由图象可知:不等式kx+b>![]() 的解集;
的解集;
(3)根据![]() 以及三角形的面积公式即可.
以及三角形的面积公式即可.
(1)∵点C(6,-1)在反比例函数![]() 的图象上,
的图象上,
所以![]() ,
,
∴m=-6,
∴反比例函数的解析式为![]() ,
,
∵点D在反比例函数![]() 的图象上,且DE=3,
的图象上,且DE=3,
∴![]()
∴x=-2,
∴点D的坐标为(-2,3),
∵C、D两点在直线y=kx+b上,
所以![]() ,
,
解得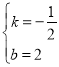
所以一次函数的解析式为:![]()
(2)由图象可知:不等式kx+b>![]() 的解集为:x<-2或0<x<6.
的解集为:x<-2或0<x<6.
(3)如图:连接OC、OD
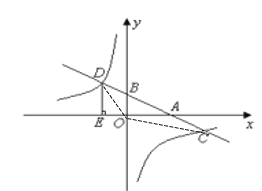
当x=0时,y=2
∴B(0,2)
∴OB=2
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
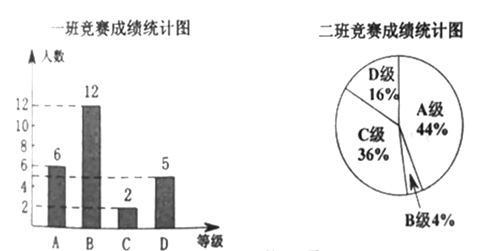
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)