��Ŀ����
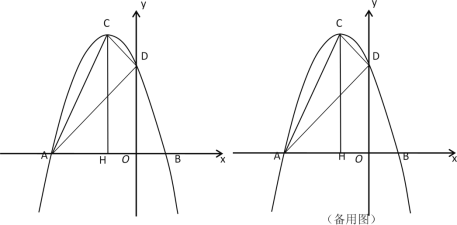
����Ŀ����ͼ����֪�����ߵĶ�������ΪM(1��4)���Ҿ�����N(2��3)����x�ύ��A��B����(��A�ڵ�B���)����y�ύ�ڵ�C��
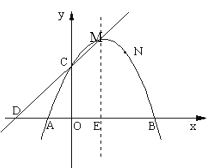
(1)�������ߵĽ���ʽ����A��B��C�����ꣻ
(2)��ֱ��y=kx+t����C��M���㣬����x�ύ�ڵ�D��̽�����ж��ı���CDAN���������ı��Σ�������õ��Ľ�������֤����
(3)ֱ��y=mx+2�������߽���T��Q���㣮�Ƿ����������ʵ��m��ʹ���߶�TQΪֱ����Բǡ�ù�����ԭ�㣬�����ڣ������m��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1)![]() ��A(-1��0)��B(3��0)��C(0��3)�� (2)�ı���CDAN��ƽ���ı��Σ�֤����������(3)���ڣ�m=
��A(-1��0)��B(3��0)��C(0��3)�� (2)�ı���CDAN��ƽ���ı��Σ�֤����������(3)���ڣ�m=![]()
��������
(1)���ݶ���ʽ�������߽���ʽΪ![]() (
(![]() )2+4����N(2��3)������
)2+4����N(2��3)������![]() ��ȷ�������߽���ʽ�����������߽���ʽ���A��B��C�����ꣻ
��ȷ�������߽���ʽ�����������߽���ʽ���A��B��C�����ꣻ
(2)����M��C����������ֱ��![]() ����ʽ���ó�D�����꣬���߶�AD����C��N���������֪CN��
����ʽ���ó�D�����꣬���߶�AD����C��N���������֪CN��![]() �ᣬ����CN��֤��CN��ADƽ������ȣ��ж϶��ı���CDAN��ƽ���ı��Σ�
�ᣬ����CN��֤��CN��ADƽ������ȣ��ж϶��ı���CDAN��ƽ���ı��Σ�
(3)���ڣ���ͼ��T(![]() ��
��![]() )��Q(
)��Q(![]() ��
��![]() )���ֱ��T��Q��TF��
)���ֱ��T��Q��TF��![]() �ᣬQG��
�ᣬQG��![]() �ᣬ����ֱ��TQ����ʽ�������߽���ʽ���ɵ�
�ᣬ����ֱ��TQ����ʽ�������߽���ʽ���ɵ�![]() ��
��![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ�������߶�TQΪֱ����Բǡ�ù�����ԭ��ʱ����TOQ=90�������û����ϵ��֤��TOF�ס�QOG���������Ʊȵó��߶ι�ϵ�����
֮��Ĺ�ϵ�������߶�TQΪֱ����Բǡ�ù�����ԭ��ʱ����TOQ=90�������û����ϵ��֤��TOF�ס�QOG���������Ʊȵó��߶ι�ϵ�����![]() ��
��![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ��m��ֵ��
֮��Ĺ�ϵ��m��ֵ��
(1)�����ߵĶ�������ΪM(1��4)���������߽���ʽΪ![]() )2+4��
)2+4��
��N(2��3)���룬��![]() (2-1)2+4=3�����
(2-1)2+4=3�����![]() ��
��
�������߽���ʽΪ![]() )2+4����
)2+4����![]() ��
��
��![]() ����
����![]() �����C������Ϊ(0��3)��
�����C������Ϊ(0��3)��
��![]() ����
����![]()
��ã�![]() ��3�����A������Ϊ(-1��0)����B������Ϊ(3��0)��
��3�����A������Ϊ(-1��0)����B������Ϊ(3��0)��
(2)�ı���CDAN��ƽ���ı��Σ�
���ɣ�
����C(0��3)��M(1��4)������ֱ��![]() �У���
����![]() ��
��
���![]() ��
��
��ֱ��CM����ʽΪ![]() �����D������Ϊ(-3��0)��
�����D������Ϊ(-3��0)��
��C(0��3)��N(2��3)��
��CN��x�ᣬ��![]() ��
��
�֡�A(-1��0)��D(-3��0)��
��AD=-1-(-3)=2��
���ı���CDAN��ƽ���ı��Σ�
(3)���ڣ�
��ͼ��T(![]() ��
��![]() )��Q(
)��Q(![]() ��
��![]() )���ֱ��T��Q��TF��
)���ֱ��T��Q��TF��![]() �ᣬQG��
�ᣬQG��![]() �ᣬ
�ᣬ
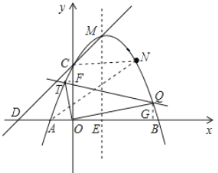
����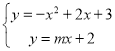 ��
��
������![]() ��
��
��![]() ��
��![]() ��
��
�����߶�TQΪֱ����Բǡ�ù�����ԭ��ʱ����TOQ=90����
���TOF+��FOQ=��FOQ+��QOB=90����
���TOF=��QOB������TFO=��QGO=90����
���TOF�ס�QOG��
��![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
�����ã�![]() ��
��
��![]() ����������
����������![]() ��
��
���![]() ��
��
�ʴ���ʵ��![]() ʹ���߶�TQΪֱ����Բ������ԭ�㣮
ʹ���߶�TQΪֱ����Բ������ԭ�㣮

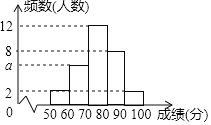
����Ŀ��Ϊ��һ���ƶ���������ѧУ����״��������������ع����������ְ����ѧ���ռ�����״���������������֪ʶ������ʦ����Уǰ��������ȫ�����������Ϻÿ�ѧ��һ�Σ�ʡ������Ҫ���������ѧУ����ѧϰ������ϣ�ij��ѧΪ�˽�ѧ����ѧϰ�ɹ�����ѧ������������״����������֪ʶ���ԣ�������������ߡ��������꼶����ȡ20��ѧ���Ĵ���ɼ�����λ���֣�����ͳ�Ʒ������������£�
�ռ�����
���꼶��
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
���꼶��
80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
��������
�ɼ� |
|
|
|
|
���꼶 | 2 | 5 |
|
|
���꼶 | 3 | 7 | 5 | 5 |
��������
ͳ���� | ƽ���� | ��λ�� | ���� |
���꼶 | 85��75 | 87��5 |
|
���꼶 | 83��5 |
| 80 |
Ӧ������
��1����գ�![]() __________��
__________��![]() __________��
__________��![]() __________��
__________��![]() __________��
__________��
��2������ͳ�����ݣ�����Ϊ������״����������֪ʶ���ո��õ��꼶��__________��
��3�������꼶����500�˲�����������ư��꼶�ɼ�����90�ֵ�������
��4������β����У����꼶ѧ���������꼶ѧ���ҵijɼ�����85�֣����ж������ڸ����꼶������˭����ǰ����˵�����ɣ�