题目内容
如图,抛物线y1=a(x+2)2-3与y2=
(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2-y1=4
④2AB=3AC.
其中正确结论是______.

| 1 |
| 2 |
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2-y1=4
④2AB=3AC.
其中正确结论是______.

①∵抛物线y2=
(x-3)2+1开口向上,顶点坐标在x轴的上方,
∴无论x取何值,y2的值总是正数,故本小题正确;
②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=
,故本小题错误;
③由两函数图象可知,抛物线y1=a(x+2)2-3解析式为y1=
(x+2)2-3,当x=0时,y1=
(0+2)2-3=-
,y2=
(0-3)2+1=
,故y2-y1=
+
=
,故本小题错误;
④∵物线y1=a(x+2)2-3与y2=
(x-3)2+1交于点A(1,3),
∴y1的对称轴为x=-2,y2的对称轴为x=3,
∴B(-5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故本小题正确.
故答案为:①④.
| 1 |
| 2 |
∴无论x取何值,y2的值总是正数,故本小题正确;
②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=
| 2 |
| 3 |
③由两函数图象可知,抛物线y1=a(x+2)2-3解析式为y1=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 1 |
| 3 |
| 35 |
| 6 |
④∵物线y1=a(x+2)2-3与y2=
| 1 |
| 2 |
∴y1的对称轴为x=-2,y2的对称轴为x=3,
∴B(-5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故本小题正确.
故答案为:①④.

练习册系列答案
相关题目
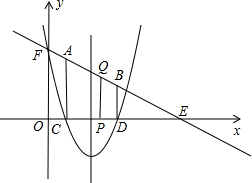 求四边形PQFC的面积S与t之间的函数关系式,并确定t的取值范围.
求四边形PQFC的面积S与t之间的函数关系式,并确定t的取值范围.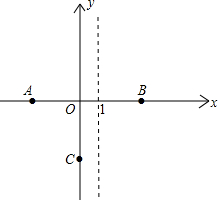

 点B的左侧),与y轴交于点C.
点B的左侧),与y轴交于点C.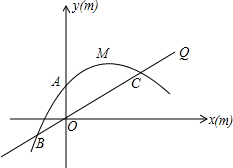 为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.
为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.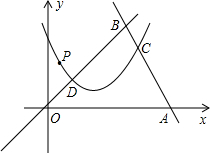
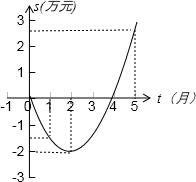 来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: