题目内容
某隧道根据地质结构要求其横截面要建成抛物线拱形,计划路面水平宽度AB=12m,根据施工需要,选取AB的中点D为支撑点,搭一个正三角形支架ADC,C点在抛物线上(如图所示),过C竖一根立柱CO⊥AB于O.
(1)求立柱CO的长度;
(2)以O点为坐标原点,AB所在的直线为横坐标轴,自己画出平面直角坐标系,写出A、B、C三点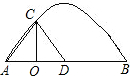 的坐标(坐标轴上的一个长度单位为1m);
的坐标(坐标轴上的一个长度单位为1m);
(3)求经过A、B、C三点的抛物线方程;
(4)请帮助施工技术员计算该抛物线拱形的高.
(1)求立柱CO的长度;
(2)以O点为坐标原点,AB所在的直线为横坐标轴,自己画出平面直角坐标系,写出A、B、C三点
 的坐标(坐标轴上的一个长度单位为1m);
的坐标(坐标轴上的一个长度单位为1m);(3)求经过A、B、C三点的抛物线方程;
(4)请帮助施工技术员计算该抛物线拱形的高.
(1)△ADC是边长为6的正三角形,CO是AD边上的高,
∴AO=OD=3,
CO2=
=
=3
(米)
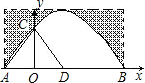
(2)画出平面直角坐标系.
则A、(-3,0),B、(9,0),C、(0,3
)
(3)CO=3
,设抛物线方程为y=ax2+bx+3
把A(-3,0)、B(9,0)代入抛物线方程有
解得
故y=-
x2+
x+3
(4)y=-
x2+
x+3
=-
(x2-6x-27)=-
(x-3)2+4
.
故y的最大值是4
,即该抛物线拱形的高是4
m.
∴AO=OD=3,
CO2=
| AC2-AO2 |
| 36-9 |
| 3 |
(2)画出平面直角坐标系.
则A、(-3,0),B、(9,0),C、(0,3
| 3 |
(3)CO=3
| 3 |
| 3 |
把A(-3,0)、B(9,0)代入抛物线方程有
|
解得
|
故y=-
| ||
| 9 |
2
| ||
| 3 |
| 3 |
(4)y=-
| ||
| 9 |
2
| ||
| 3 |
| 3 |
| ||
| 9 |
| ||
| 9 |
| 3 |
故y的最大值是4
| 3 |
| 3 |


练习册系列答案
相关题目
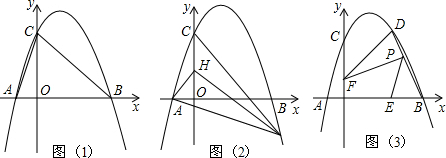

 点B的左侧),与y轴交于点C.
点B的左侧),与y轴交于点C.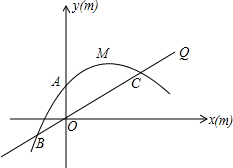 为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.
为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.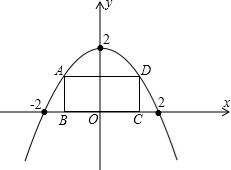 x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.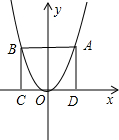 点的坐标(用含有a、b、c的代数式表示)
点的坐标(用含有a、b、c的代数式表示)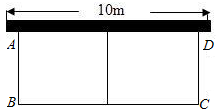 篱笆,一面靠墙(墙长为10m),设花圃宽AB为x(m),面积为S(m2).
篱笆,一面靠墙(墙长为10m),设花圃宽AB为x(m),面积为S(m2).