题目内容
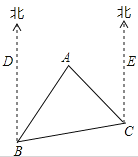
【题目】如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F.
(1) CD与EF平行吗？为什么？
(2)如果∠1=∠2，且∠3=115°，求∠ACB的度数．
【答案】（1）平行；（2）115°.
【解析】
(1)先根据垂直的定义得到∠CDB＝∠EFB＝90°，然后根据同位角相等，两直线平行可判断EF∥CD；
(2)由EF∥CD，根据平行线的性质得∠2＝∠BCD，而∠1＝∠2，所以∠1＝∠BCD，根据内错角相等，两直线平行得到DG∥BC，所以∠ACB＝∠3=115°.
解:(1)CD与EF平行.理由如下:
CD⊥AB，EF⊥AB，
∴∠CDB＝∠EFB＝90°
∴EF∥CD
(2) 如图：
EF∥CD，
∴∠2＝∠BCD
又∠1＝∠2，
∴∠1＝∠BCD
∴DG∥BC，
∴∠ACB＝∠3＝115°.
练习册系列答案
名校课堂系列答案
相关题目
