ЬтФПФкШн
ЁОЬтФПЁПвбжЊЕШБп![]() ЕФБпГЄЮЊ2ЃЌЯжНЋЕШБп
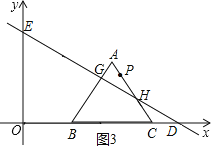
ЕФБпГЄЮЊ2ЃЌЯжНЋЕШБп![]() ЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕуBКЭдЕужиКЯЃЌЕуCдкxжсе§ЗНЯђЩЯЃЌжБЯпНЛxжсгкЕуDЃЌНЛyжсгкЕуEЃЌЧв
ЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕуBКЭдЕужиКЯЃЌЕуCдкxжсе§ЗНЯђЩЯЃЌжБЯпНЛxжсгкЕуDЃЌНЛyжсгкЕуEЃЌЧв![]() ШчЭМ
ШчЭМ![]() ЃЌЯжНЋЕШБп
ЃЌЯжНЋЕШБп![]() ДгЭМ1ЕФЮЛжУбиxжсе§ЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШвЦЖЏЃЌБпABЁЂACЗжБ№гыЯпЖЮDEНЛгкЕуGЁЂ
ДгЭМ1ЕФЮЛжУбиxжсе§ЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШвЦЖЏЃЌБпABЁЂACЗжБ№гыЯпЖЮDEНЛгкЕуGЁЂ![]() ШчЭМ
ШчЭМ![]() ЃЌЭЌЪБЕуPДг
ЃЌЭЌЪБЕуPДг![]() ЕФЖЅЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиелЯп
ЕФЖЅЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиелЯп![]() дЫЖЏ
дЫЖЏ![]() ЕБЕуPдЫЖЏЕНCЪБМДЭЃжЙЛюЖЏЃЌ
ЕБЕуPдЫЖЏЕНCЪБМДЭЃжЙЛюЖЏЃЌ![]() вВЫцжЎЭЃжЙвЦЖЏЃЌЩш
вВЫцжЎЭЃжЙвЦЖЏЃЌЩш![]() ЦНвЦЕФЪБМфЮЊ
ЦНвЦЕФЪБМфЮЊ![]() ЃЎ
ЃЎ
![]() ЪдЧѓжБЯпDEЕФНтЮіЪНЃЛ
ЪдЧѓжБЯпDEЕФНтЮіЪНЃЛ
![]() ЕБЕуPдкЯпЖЮACЩЯдЫЖЏЪБЃЌЩшЕуPгыЕуHЕФОрРыЮЊyЃЌЧѓyгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђЃЛ
ЕБЕуPдкЯпЖЮACЩЯдЫЖЏЪБЃЌЩшЕуPгыЕуHЕФОрРыЮЊyЃЌЧѓyгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђЃЛ
![]() ЕБЕуPдкЯпЖЮABЩЯдЫЖЏЪБЃЌ
ЕБЕуPдкЯпЖЮABЩЯдЫЖЏЪБЃЌ![]() жаЧЁКУгавЛИіНЧЕФЖШЪ§ЮЊ
жаЧЁКУгавЛИіНЧЕФЖШЪ§ЮЊ![]() ЃЌЧыжБНгаДГіtЕФжЕЃЌВЛБиаДЙ§ГЬЃЎ
ЃЌЧыжБНгаДГіtЕФжЕЃЌВЛБиаДЙ§ГЬЃЎ

ЁОД№АИЁП![]() ЕБдЫЖЏЪБМфtЮЊ
ЕБдЫЖЏЪБМфtЮЊ![]() УыЛђ
УыЛђ![]() УыЛђ1УыЪБЃЌ
УыЛђ1УыЪБЃЌ![]() жаЧЁКУгавЛИіНЧЕФЖШЪ§ЮЊ
жаЧЁКУгавЛИіНЧЕФЖШЪ§ЮЊ![]()
ЁОНтЮіЁП
![]() ИљОнЕШБпШ§НЧаЮЕФаджЪНсКЯ
ИљОнЕШБпШ§НЧаЮЕФаджЪНсКЯ![]() ЃЌПЩЕУГі
ЃЌПЩЕУГі![]() ЃЌНсКЯABЕФГЄЖШПЩЕУГіOEЁЂODЕФГЄЖШЃЌНјЖјПЩЕУГіЕуDЁЂEЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпDEЕФНтЮіЪНЃЛ
ЃЌНсКЯABЕФГЄЖШПЩЕУГіOEЁЂODЕФГЄЖШЃЌНјЖјПЩЕУГіЕуDЁЂEЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпDEЕФНтЮіЪНЃЛ
![]() ИљОнЕуPЁЂCЕФдЫЖЏЫйЖШПЩЕУГіPAЁЂCDЕФжЕЃЌгЩ
ИљОнЕуPЁЂCЕФдЫЖЏЫйЖШПЩЕУГіPAЁЂCDЕФжЕЃЌгЩ![]() ЁЂ
ЁЂ![]() ПЩЕУГі
ПЩЕУГі![]() ЃЌНјЖјПЩЕУГіCHЕФГЄЃЌдйИљОн
ЃЌНјЖјПЩЕУГіCHЕФГЄЃЌдйИљОн![]() МДПЩевГіyгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
МДПЩевГіyгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ЗжЕуPЁЂAжиКЯМАЕуPЁЂAВЛжиКЯСНжжЧщПіПМТЧЃК
ЗжЕуPЁЂAжиКЯМАЕуPЁЂAВЛжиКЯСНжжЧщПіПМТЧЃК![]() ЕБЕуPЁЂAжиКЯЪБЃЌМД
ЕБЕуPЁЂAжиКЯЪБЃЌМД![]() ЪБЃЌЗћКЯЬтвтЃЌгЩ
ЪБЃЌЗћКЯЬтвтЃЌгЩ![]() ПЩЧѓГіtжЕЃЛ
ПЩЧѓГіtжЕЃЛ![]() ЕБЕуPЁЂAВЛжиКЯЪБЃЌЗж
ЕБЕуPЁЂAВЛжиКЯЪБЃЌЗж![]() КЭ
КЭ![]() СНжжЧщПіПМТЧЃЌЭЈЙ§НтжБНЧШ§НЧаЮМДПЩЧѓГіtжЕ
СНжжЧщПіПМТЧЃЌЭЈЙ§НтжБНЧШ§НЧаЮМДПЩЧѓГіtжЕ![]() злЩЯМДПЩЕУГіНсТлЃЎ
злЩЯМДПЩЕУГіНсТлЃЎ
НтЃК![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЕуDЕФзјБъЮЊ
ЕуDЕФзјБъЮЊ![]() ЃЌЕуEЕФзјБъЮЊ
ЃЌЕуEЕФзјБъЮЊ![]()
ЩшжБЯпDEЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
НЋ![]() ЁЂ
ЁЂ![]() ДњШы
ДњШы![]() ЃЌЕУЃК
ЃЌЕУЃК
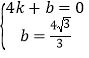 ЃЌНтЕУЃК
ЃЌНтЕУЃК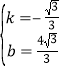 ЃЌ
ЃЌ
![]() жБЯпDEЕФНтЮіЪНЮЊ
жБЯпDEЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
![]() ШчЭМ3ЃЌ
ШчЭМ3ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЕуPдкACЩЯЃЌ
ЕуPдкACЩЯЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
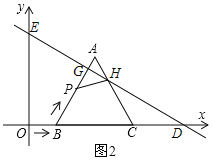
![]() ШчЭМ2ЃЌ
ШчЭМ2ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЕБЕуPЁЂAжиКЯЪБЃЌМД
ЕБЕуPЁЂAжиКЯЪБЃЌМД![]() ЪБЃЌЗћКЯЬтвтЃЌ
ЪБЃЌЗћКЯЬтвтЃЌ
ДЫЪБ![]() ЃЛ
ЃЛ
![]() ЕБЕуPЁЂAВЛжиКЯЪБЃЌ
ЕБЕуPЁЂAВЛжиКЯЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЛ
ЃЛ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКЕБдЫЖЏЪБМфtЮЊ![]() УыЛђ
УыЛђ![]() УыЛђ1УыЪБЃЌ
УыЛђ1УыЪБЃЌ![]() жаЧЁКУгавЛИіНЧЕФЖШЪ§ЮЊ
жаЧЁКУгавЛИіНЧЕФЖШЪ§ЮЊ![]() ЃЎ
ЃЎ

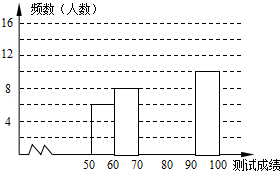
ЁОЬтФПЁПЁАЩЭжаЛЊЪЋДЪЃЌбАЮФЛЏЛљвђЃЌЦЗЩњЛюжЎУРЁБЃЌФГаЃОйАьСЫЪзНьЁАжаЙњЪЋДЪДѓЛсЁБЃЌОбЁАЮКѓга50УћбЇЩњВЮМгОіШќЃЌет50УћбЇЩњЭЌЪБФЌаД50ЪзЙХЪЋДЪЃЌШєУПе§ШЗФЌаДГівЛЪзЙХЪЋДЪЕУ2ЗжЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃК
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 50ЁмxЃМ60 | 6 |
Ек2зщ | 60ЁмxЃМ70 | 8 |
Ек3зщ | 70ЁмxЃМ80 | 14 |
Ек4зщ | 80ЁмxЃМ90 | a |
Ек5зщ | 90ЁмxЃМ100 | 10 |
ЧыНсКЯЭМБэЭъГЩЯТСаИїЬтЃК
ЃЈ1ЃЉЂйЧѓБэжаaЕФжЕЃЛЂкЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉШєВтЪдГЩМЈВЛЕЭгк80ЗжЮЊгХауЃЌдђБОДЮВтЪдЕФгХауТЪЪЧЖрЩйЃП
ЃЈ3ЃЉЕк5зщ10УћЭЌбЇжаЃЌга4УћФаЭЌбЇЃЌЯжНЋет10УћЭЌбЇЦНОљЗжГЩСНзщНјааЖдПЙСЗЯАЃЌЧв4УћФаЭЌбЇУПзщЗжСНШЫЃЌЧѓаЁУїгыаЁЧПСНУћФаЭЌбЇФмЗждкЭЌвЛзщЕФИХТЪЃЎ