题目内容
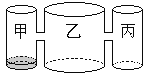
【题目】实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，，用两个相同的管子在容器的5cm高度处连通（即管子底端离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升
cm，则开始注入 分钟的水量后，甲与乙的水位高度之差是0．5cm．
【答案】
，
，
【解析】
试题∵甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1:2:1，∴甲、乙、丙三个圆柱形容器的底面积之比为1：4：1，∵每分钟同时向乙和丙注入相同量的水，注水1分钟，乙的水位上升
cm，∴注水1分钟，丙的水位上升
cm，
当甲比乙高0．5cm时，此时乙中水位高0．5cm，用时0．5÷=分；
当丙的高度到5cm时，此时用时为5÷
=
分，此时乙中水高
=
<1+0．5，在这之后丙中的水流入乙中，乙每分钟水位上升
cm，1．5-=
，
分，即开始注水后乙比甲高0．5cm的用时为
分；
当乙的水位达到5cm时开始流向甲，此时用时为
=
分，甲水位每分上升
cm，当甲的水位高为4．5cm时，乙比甲高0．5cm，此时用时
=分；
综上，开始注入
分钟的水量后，甲与乙的水位高度之差是0．5cm
【题目】某校为了了解学生大课间活动的跳绳情况，随机抽取了50名学生每分钟跳绳的次数进行统计，把统计结果绘制成如表和直方图．
次数 | 70≤x＜90 | 90≤x＜110 | 110≤x＜130 | 130≤x＜150 | 150≤x＜170 |
人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息，回答下列问题：
（1）本次调查的样本容量是；
（2）本次调查中每分钟跳绳次数达到110次以上（含110次）的共有的共有人；
（3）根据上表的数据补全直方图；
（4）如果跳绳次数达到130次以上的3人中有2名女生和一名男生，学校从这3人中抽取2名学生进行经验交流，求恰好抽中一男一女的概率（要求用列表法或树状图写出分析过程）．
