题目内容
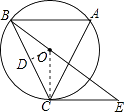
【题目】如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E. 
(1)求∠BCE的度数;
(2)若⊙O半径为3,求BE长.
【答案】
(1)解:连接OC,∵∠A=60°,∴∠BOC=120°,
又∵OB=OC,∴∠OCB=∠OBC=30°,
∵EC切⊙O于E,∴∠OCE=90°,
∴∠ECB=120°
(2)解:过点O作OD⊥BC于点D,
∵∠A=60°,
∴∠BOC=120°,
又∵∠CBE=∠BOC,
∴△BOC∽△BCE,
∴ ![]() =
= ![]()
∴BC2=BOBE;
∵BO=3,∠OBD=30°,
∴BD=BOcos30°= ![]() ,
,
∴BC=3 ![]() ,
,
∴(3 ![]() )2=3BE,
)2=3BE,
∴BE=9.
【解析】(1)利用切线的性质结合等腰三角形的性质得出∠OCE=90°,∠OCB=∠OBC=30°,进而求出∠BCE的度数;(2)利用相似三角形的判定与性质得出△BOC∽△BCE,进而得出 ![]() =
= ![]() ,进而得出答案.
,进而得出答案.
【考点精析】通过灵活运用切线的性质定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目