Question

【题目】阅读材料：

在平面直角坐标系xOy中，点P（x0，y0）到直线Ax+By+C=0的距离公式为：d=．

例如：求点P0（0，0）到直线4x+3y﹣3=0的距离．

解：由直线4x+3y﹣3=0知，A=4，B=3，C=﹣3，

∴点P0（0，0）到直线4x+3y﹣3=0的距离为d==．

根据以上材料，解决下列问题：

问题1：点P1（3，4）到直线y=﹣x+的距离为 ；

问题2：已知：⊙C是以点C（2，1）为圆心，1为半径的圆，⊙C与直线y=﹣x+b相切，求实数b的值；

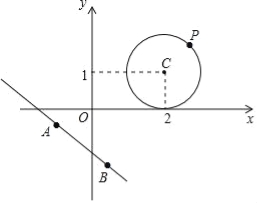
问题3：如图，设点P为问题2中⊙C上的任意一点，点A，B为直线3x+4y+5=0上的两点，且AB=2，请求出S△ABP的最大值和最小值．

Answer 1

【答案】（1）4；（2）b=5或15；（3）最大值为4，最小值为2.

【解析】试题分析：（1）根据点到直线的距离公式就是即可；（2）根据点到直线的距离公式，列出方程即可解决问题;（3）求出圆心C到直线3x+4y+5=0的距离，求出⊙C上点P到直线3x+4y+5=0的距离的最大值以及最小值即可解决问题．

试题解析：

（1）点P1（3，4）到直线3x+4y﹣5=0的距离d==4；

（2）∵⊙C与直线y=﹣x+b相切，⊙C的半径为1，

∴C（2，1）到直线3x+4y﹣b=0的距离d=1，

∴=1，

解得b=5或15．

（3）点C（2，1）到直线3x+4y+5=0的距离d==3，

∴⊙C上点P到直线3x+4y+5=0的距离的最大值为4，最小值为2，

∴S△ABP的最大值=×2×4=4，S△ABP的最小值=×2×2=2．