Question

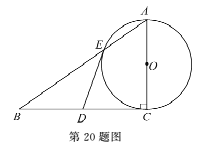
【题目】如图，已知RtΔABC,∠C=90°，D为BC的中点.以AC为直径的圆O交AB于点E.

（1）求证：DE是圆O的切线.

(2)若AE:EB=1:2,BC=6，求AE的长.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】：

试题分析：利用思路：知（连）半径，证垂直，证明DE是圆O的切线；利用射影定理或相似三角形证明：BE2=BE×BA,再列方程，求AE的长.

试题解析：(1)如图所示，连接OE，CE

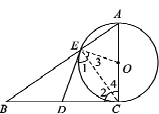
∵AC是圆O的直径

∴∠AEC=∠BEC=90°

∵D是BC的中点

∴ED＝BC＝DC

∴∠1=∠2

∵OE=OC

∴∠3=∠4

∴∠1+∠3=∠2+∠4,即∠OED=∠ACD

∵∠ACD=90°

∴∠OED=90°,即OE⊥DE

又∵E是圆O上的一点

∴DE是圆O的切线.

（2）由（1）知∠BEC=90°

在RtΔBEC与RtΔBCA中，∠B为公共角，

∴ΔBEC∽ΔBCA

∴

即BC2=BE×BA

∵AE:EB=1：2，设AE=x，则BE＝2x，BA=3x.

又∵BC=6

∴62=2x×3x

∴x=,即AE=.