题目内容
【题目】如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y= ![]() (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 . 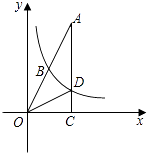
【答案】y=2x
【解析】解:设OC=a, ∵点D在y= ![]() 上,
上,
∴CD= ![]() ,
,
∵△OCD∽△ACO,
∴ ![]() =
= ![]() ,
,
∴AC= ![]() =
= ![]() ,
,
∴点A(a, ![]() ),
),
∵点B是OA的中点,
∴点B的坐标为( ![]() ,
, ![]() ),
),
∵点B在反比例函数图象上,
∴ ![]() =
= ![]() ,
,
∴ ![]() =2k2 ,
=2k2 ,
∴a4=4k2 ,
解得,a2=2k,
∴点B的坐标为( ![]() ,a),
,a),
设直线OA的解析式为y=mx,
则m ![]() =a,
=a,
解得m=2,
所以,直线OA的解析式为y=2x.
所以答案是:y=2x.
【考点精析】认真审题,首先需要了解相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形).

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目