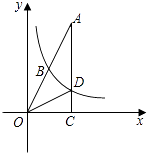题目内容
【题目】如图，在平面直角坐标系中，ABCD的顶点B，C在x轴上，A，D两点分别在反比例函数y=﹣ 
（x＜0）与y= 
（x＞0）的图象上，则ABCD的面积为 ． 
【答案】4
【解析】解：连接OA、OD，如图， ∵四边形ABCD为平行四边形，
∴AD垂直y轴，
∴S△OAE= 
×|﹣3|= 
，S△ODE= ×|1|= ，
∴S△OAD=2，
∴ABCD的面积=2S△OAD=4．
所以答案是4．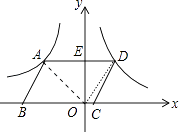
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识，掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积，以及对平行四边形的性质的理解，了解平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
练习册系列答案
相关题目
