题目内容
【题目】如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2. 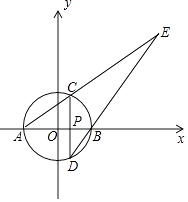
(1)求点P的坐标;
(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.
【答案】
(1)如图,作EF⊥y轴于F,DC的延长线交EF于H.设H(m,n),则P(m,0),PA=m+3,PB=3﹣m.
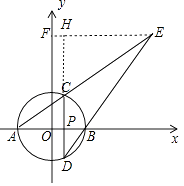
∵EH∥AP,
∴△ACP∽△ECH,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴CH=2n,EH=2m=6,
∵CD⊥AB,
∴PC=PD=n,
∵PB∥HE,
∴△DPB∽△DHE,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴m=1,
∴P(1,0).
(2)由(1)可知,PA=4,HE=8,EF=9,
连接OP,在Rt△OCP中,PC= ![]() =2
=2 ![]() ,
,
∴CH=2PC=4 ![]() ,PH=6
,PH=6 ![]() ,
,
∴E(9,6 ![]() ),
),
∵抛物线的对称轴为CD,
∴(﹣3,0)和(5,0)在抛物线上,设抛物线的解析式为y=a(x+3)(x﹣5),把E(9,6 ![]() )代入得到a=
)代入得到a= ![]() ,
,
∴抛物线的解析式为y= ![]() (x+3)(x﹣5),即y=
(x+3)(x﹣5),即y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]()
【解析】(1)如图,作EF⊥y轴于F,DC的延长线交EF于H.设H(m,n),则P(m,0),PA=m+3,PB=3﹣m.首先证明△ACP∽△ECH,推出 ![]() =
= ![]() =
= ![]() =
= ![]() ,推出CH=2n,EH=2m=6,再证明△DPB∽△DHE,推出
,推出CH=2n,EH=2m=6,再证明△DPB∽△DHE,推出 ![]() =
= ![]() =
= ![]() =
= ![]() ,可得
,可得 ![]() =
= ![]() ,求出m即可解决问题;(2)由题意设抛物线的解析式为y=a(x+3)(x﹣5),求出E点坐标代入即可解决问题;
,求出m即可解决问题;(2)由题意设抛物线的解析式为y=a(x+3)(x﹣5),求出E点坐标代入即可解决问题;

练习册系列答案
相关题目