题目内容
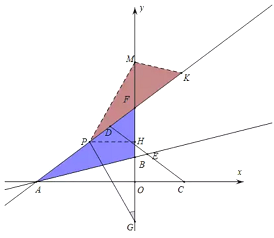
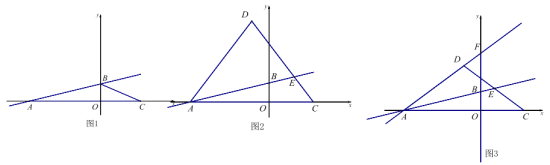
【题目】已知，如图，在平面直角坐标系中，直线AB：
交x轴于点A（-4，0），交y轴于点B，点C（2，0）．
（1）如图1，求直线AB的解析式；
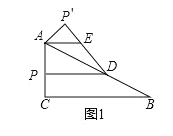
（2）如图2，点D为第二象限内一点，且AD=DC，DC交直线AB于点E，设DE：EC=m，点D的纵坐标为d，求d与m的函数关系式（不要求写出自变量的取值范围）；
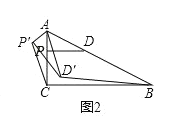
（3）如图3，在（2）的条件下，直线AD交y轴于点F，点P为线段AF上一点，G为y轴负半轴上一点，PG=AB，且∠PGF+∠BAF=∠AFB，当m=1时，求点G的坐标．
【答案】（1）
；（2）
；（3）
【解析】
（1）将点A（4，0）代入
，求出b＝1即可；
（2）由已知可得D（1，d），求出CD的直线解析式为
，再由E是两直线的交点，求出E（
，
），过点D作DQ⊥x轴于Q，作EN∥x轴交DQ于N，则
，由EC：CD＝1：（m＋1），即可求出d＝
；
（3）过点P作PH⊥y轴于点H，截取HM＝HG，求出直线AD的解析式为
，则F（0，3），tan∠AFB＝
，所以FH＝
PH，易证Rt△PHG≌RtPHM，由角的关系得到∠MPF＝∠FAB，构造△PKM≌△AFB，可得FB＝MK＝MF，求出FB＝MK＝MF＝2，在Rt△PHM中，根据PM2＝PH2＋MH2，求出PH＝
，FH＝
，最后求出OG＝HGOH＝
，即可求解．
解：（1）将点A（4，0）代入，得
，
∴b＝1，
∴直线AB的解析式为；
（2）∵AC＝6，AD＝DC，
∴D的横坐标为1，
∵点D的纵坐标为d，
设直线CD的解析式为
，
代入D（1，d），C（2，0）得：
，解得：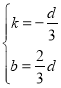
，
∴直线CD的解析式为，
联立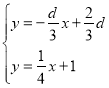
，可得E（，），
如图，过点D作DQ⊥x轴于Q，作EN∥x轴交DQ于N，
则，
∵DE：EC＝m，
∴EC：CD＝1：（m＋1），
∴
，
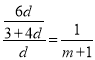∴d＝；
（3）如图，过点P作PH⊥y轴于点H，截取HM＝HG，
∵m＝1，
∴d＝
，
∴D（1，），
设直线AD的解析式为
，
代入A（4，0），D（1，）得：
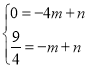，解得：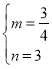
，
∴直线AD的解析式为，
∴F（0，3），
∴tan∠AFB＝，
∴
，
∴FH＝PH，
易证Rt△PHG≌Rt△PHM（HL），
∴PG＝PM＝AB，∠PGH＝∠PMH，
∴∠AFB＝∠PMF＋∠MPF，
∵∠PGF＋∠BAF＝∠AFB，
∴∠MPF＝∠FAB，
构造△PKM≌△AFB，
则∠MFK＝∠AFB＝∠PKM，
∴FB＝MK＝MF，
∵OF＝3，OB＝1，
∴FB＝MK＝MF＝2，
在Rt△PHM中，PM2＝PH2＋MH2，
∵AB＝
，
∴17＝PH2＋（2＋PH）2，
∴PH＝，
∴FH＝，
∴HG＝HM＝2＋＝
，OH＝3＝
，
∴OG＝HGOH＝，
∴G（0，
）．
