题目内容
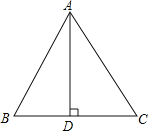
【题目】![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上不与点
上不与点![]() 重合的一点,作
重合的一点,作![]() 交边
交边![]() 于
于![]() 点.
点.
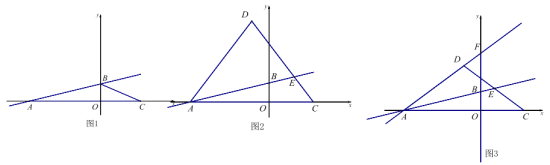
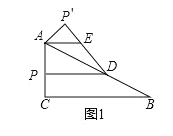
![]() 如图1,将
如图1,将![]() 沿直线
沿直线![]() 翻折,得到
翻折,得到![]() ,作
,作![]() .求证:
.求证:![]() ;
;
![]() 将
将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
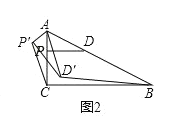
①如图2,当点![]() 在
在![]() 内部时,连接
内部时,连接![]() 和
和![]() ,求证:
,求证:![]() ;
;
②如果![]() 连接
连接![]() 且
且![]() 那么请直接写出点
那么请直接写出点![]() 到直线
到直线![]() 的距离.
的距离.
【答案】(1)详见解析;(2)①详见解析;②点![]() 到直线
到直线![]() 的距离为
的距离为![]() 或
或![]()
【解析】
(1)由折叠的性质和平行线的性质可得∠EAD=∠ADP=∠ADP',即可得AE=DE;
(2)①由题意可证△APD∽△ACB,可得![]() ,由旋转的性质可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,
,由旋转的性质可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,![]() ,则△AP'C∽△AD'B;
,则△AP'C∽△AD'B;
②分点D'在直线BC的下方和点D'在直线BC的上方两种情况讨论,根据平行线分线段成比例,可求PD=![]() ,通过证明△AMD'≌△DPA,可得AM=PD=
,通过证明△AMD'≌△DPA,可得AM=PD=![]() ,即可求点D'到直线BC的距离.
,即可求点D'到直线BC的距离.
![]() 证明:
证明:![]() 将
将![]() 沿直线
沿直线![]() 翻折,得到
翻折,得到![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]() 旋转,
旋转,
![]() ,
,
![]() ,
,![]()
![]()
![]() 若点
若点![]() 在直线
在直线![]() 下方,如图,过点
下方,如图,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]()

![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() 旋转,
旋转,
![]() ,且
,且![]()
![]() ,
,![]() ,
,
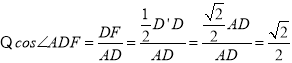
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]()
![]()
![]()
![]() ,
,
![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]()
若点![]() 在直线
在直线![]() 的上方,如图,过点
的上方,如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
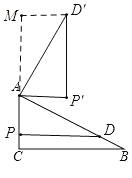
同理可证:![]() ,
,
![]()
![]()
![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]()
综上所述:点![]() 到直线
到直线![]() 的距离为
的距离为![]() 或
或![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.

小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
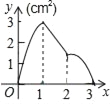
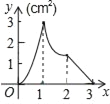
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
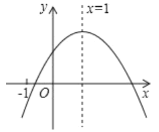
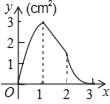
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).