题目内容
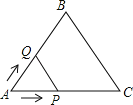
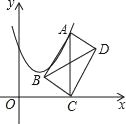
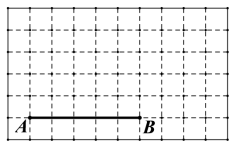
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.
(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
【答案】(1)如图所示见解析;(2)如图所示见解析;(3)![]() .
.
【解析】
(1)根据AB的长和三角形的面积即可求出点C所在的直线,然后根据AB=BC即可找出点C;
(2)以AB为直径作圆,从圆与小正方形的顶点的交点中找出满足AD>BD的点D即可;
(3)根据勾股定理计算即可.
解:(1)由图可知:AB=5,
∵△ABC 的面积为![]()
∴C到AB的距离为![]() ×2÷5=3
×2÷5=3
∴点C在与AB平行且相距3的直线上,以点B为圆心,AB的长为半径作弧,交该直线与点C,连接AC、BC,如图所示△ABC即为所求;

(2)以AB为直径作圆,从圆与小正方形的顶点的交点中找出满足AD>BD的点D即可,如图所示,△ABD即为所求;
(3)根据勾股定理![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
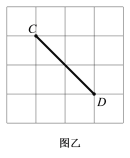
口算与应用题卡系列答案【题目】在方格纸中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图甲中,每个小正方形的边长为1,以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值;
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
(2)在图乙中,所给的方格纸大小与图甲一样,如果以线段CD为一边,作格点三角形,试填写下表,并计算出格点三角形面积的平均值;
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
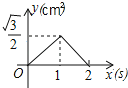
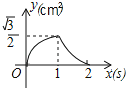
(3)如果将图乙中格点三角形面积记为s,频数记为x,根据你所填写的数据,猜测s与x之间存在哪种函数关系,并求出函数关系式.