Question

【题目】天府新区某校数学活动小组在一次活动中，对一个数学问题作如下探究：

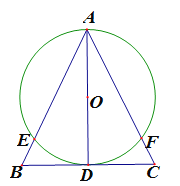
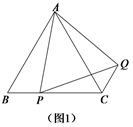
（1）问题发现：如图1，在等边△ABC中，点P是边BC上任意一点，连接AP，以AP为边作等边△APQ，连接CQ．求证：BP CQ；

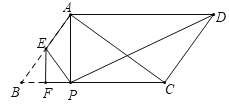
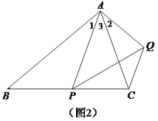
（2）变式探究：如图2，在等腰△ABC中，ABBC，点P是边BC上任意一点，以AP为腰作等腰△APQ，使AP PQ，APQ ABC，连接CQ．判断∠ABC和∠ACQ的数量关系，并说明理由；

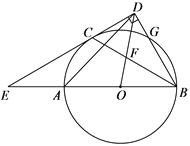
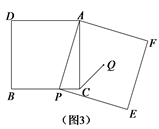
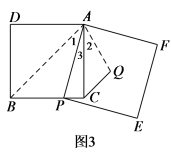
（3）解决问题：如图3，在正方形ADBC中，点P是边BC上一点，以AP为边作正方形 APEF，Q是正方形APEF的中心，连接CQ．若正方形APEF的边长为6，，求正方形ADBC的边长．

Answer 1

【答案】（1）证明见解析；（2），理由见解析；（3）正方形ADBC的边长为．

【解析】

（1）易证∠BAP＝∠CAQ，根据AB＝AC，AP＝AQ，由SAS证得△BAP≌△CAQ，即可得出结论；

（2）由等腰三角形的性质得出∠BAC＝∠PAQ，证得△BAC∽△PAQ，得出，易证∠BAP＝∠CAQ，则△BAP∽△CAQ，可得∠ABC＝∠ACQ；

（3）连接AB、AQ，由正方形的性质得出，∠BAC＝45°，，∠PAQ＝45°，易证∠BAP＝∠CAQ，则可得△ABP∽△ACQ，根据相似三角形的性质求出BP＝4，设PC＝x，则BC＝AC＝4＋x，在Rt△APC中，利用勾股定理列方程求出x，即可得出结果．

（1）证明：如图1，与都是等边三角形，

，

，

．

又，，

，

；

（2），

理由：如图2，在中，，

，

在中，，

，

，

，

，

，

又，，

，

，

∴；

（3）如图3，连接，，

正方形，

，，

又为正方形的中心，

，，

，，

，

，

，

，

，

，

设，则，

在中，，即，

解得：，

，

，

边长.