Question

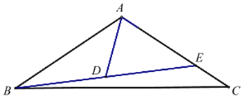
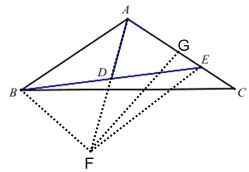
【题目】如图，△ABC中，AB=AC，E在AC上，BD=DE，tan∠DAE=3，AD=，CE=2，则线段AC的长为__________．

Answer 1

【答案】

【解析】

延长AD至F，使DF＝AD，连接BF，EF，过点F作FG⊥AC于G，则四边形ABFE是平行四边形，然后利用勾股定理求出AG＝2，FG＝6，再在Rt△EGF中，利用勾股定理求出EG即可．

解：如图，延长AD至F，使DF＝AD，连接BF，EF，过点F作FG⊥AC于G，

∵DF＝AD，BD＝DE，

∴四边形ABFE是平行四边形，

∴EF＝AB＝AC，

∵tan∠DAE＝3，

∴，即，

∵AF＝2AD＝，AG2+FG2＝AF2，

∴AG2+9AG2＝40，

∴AG＝2，FG＝6，

设EG＝x，则EF＝AC＝AG+EG+CE＝x+4，

在Rt△EGF中，EG2+FG2＝EF2，

∴x2+62＝(x+4)2，

解得：，

∴AC＝x+4＝，

故答案为：．