Question

【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．

（1）判断直线DE与⊙O的位置关系，并说明理由；

（2）如果AB=5，BC=6，求DE的长．

Answer 1

【答案】（1）相切，理由见解析；（2）DE=．

【解析】试题分析：（1）连接AD，OD，根据已知条件证得OD⊥DE即可；

（2）根据勾股定理计算即可．

解：（1）相切，

理由如下：

连接AD，OD，

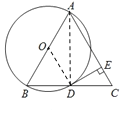
∵AB为⊙O的直径，

∴∠ADB=90°．

∴AD⊥BC．

∵AB=AC，

∴CD=BD=BC．

∵OA=OB，

∴OD∥AC．

∴∠ODE=∠CED．

∵DE⊥AC，

∴∠ODE=∠CED=90°．

∴OD⊥DE．

∴DE与⊙O相切．

（2）由（1）知∠ADC=90°，

∴在Rt△ADC中，由勾股定理得,

AD=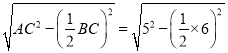=4．

∵SACD=ADCD=ACDE，

∴×4×3=×5DE．

∴DE=．