Question

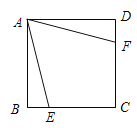
【题目】已知：如图，在平行四边形中，对角线与相交于点，过点作的垂线交边于点，与的延长线交于点，且．

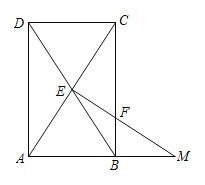
求证：（1）四边形是矩形；

（2）．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）由可得，又∠CAB=∠EAM，从而推出△ABC∽△AEM，继而推出∠ABC=∠AEM=90°，从而可得出结论；

（2）先证明△EFB∽△EBM，从而推出，得出，又DE=BE，从而可得出结果．

证明：（1）∵，∴，

又∠CAB=∠EAM，

∴△ABC∽△AEM，

∴∠ABC=∠AEM=90°，

又四边形ABCD为平行四边形，

∴四边形ABCD为矩形；

（2）∵四边形ABCD为矩形，∴AE=BE=DE=CE，

∴∠EAB=∠EBA，又∠EAB+∠M=90°，∠EBA+∠EBF=90°

∴∠M=∠EBF，

又∠FEB=∠BEM，

∴△EFB∽△EBM，

∴，

∴，

∴．