题目内容

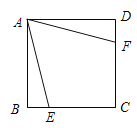
【题目】如图，在正方形ABCD中，AB=1，点E、F分别在边BC和CD上，AE＝AF，∠EAF=60°，则CF的长是____．

【答案】

【解析】

先证△ABE≌△ADF，再求tan15°的大小，可得DF的长，最终得到CF

∵四边形ABCD是正方形

∴∠B=∠D=90°，AB=AD=1

∵AE=AF

∴△ABE≌△ADF，∴∠BAE=∠DAF

∵∠EAF=60°

∴∠BAE=∠FAD=15°

∴DF=ADtan15°=tan15°

如下图，在△MNQ中，∠M=15°，∠N=90°，在MN上取一点P，使得PQ=PM

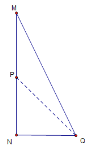
∵PQ=PM，∠M=15°

∴∠PQM=15°

∵∠N=90°，∴∠NQM=75°

∴∠NQP=60°

设NQ=x

在Rt△NPQ中，NP=，PQ=2x

在△PMQ中，PM=2x

∴在Rt△MNQ中，tan15°=tan∠M=

∴FD=

∴CF=CD-DF=

故答案为：

练习册系列答案
相关题目

【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

（1）证明与推断：

①求证：四边形CEGF是正方形；

②推断：的值为　 　：

（2）探究与证明：

将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

（3）拓展与运用：

正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2，则BC=　 　．

【题目】如图1，抛物线y＝x2+（m﹣2）x﹣2m（m＞0）与x轴交于A、B两点（A在B左边），与y轴交于点C．连接AC、BC，D为抛物线上一动点（D在B、C两点之间），OD交BC于E点．

（1）若△ABC的面积为8，求m的值；

（2）在（1）的条件下，求的最大值；

（3）如图2，直线y＝kx+b与抛物线交于M、N两点（M不与A重合，M在N左边），连MA，作NH⊥x轴于H，过点H作HP∥MA交y轴于点P，PH交MN于点Q，求点Q的横坐标．

【题目】每年的月日为世界环保日，为了提倡低碳环保，某公司决定购买台节省能源的新设备，现有甲、乙两种型号的设备可供选购.经调查：购买台甲型设备比购买台乙型设备多花万元，购买台甲型设备比购买台乙型设备少花万元.

（1）求甲、乙两种型号设备每台的价格；

（2）该公司经决定购买甲型设备不少于台，预算购买节省能源的新设备资金不超过万元，你认为该公司有哪几种购买方案；

（3）在（2）的条件下，已知甲型设备每月的产量为吨，乙型设备每月的产量为吨.若每月要求产量不低于吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.

【题目】如图，中，，点、同时从点出发，以的速度分别沿、匀速运动，当点到达点时，两点同时停止运动，设运动时间为．过点作的垂线交于点，点与点关于直线对称．

（1）当_____时，点在的平分线上；

（2）当_____时，点在边上；

（3）设与重合部分的面积为，求与之间的函数关系式，并写的取值范围．

【题目】下面所示各图是在同一直角坐标系内，二次函数y＝+（a+c）x+c与一次函数y＝ax+c的大致图象．正确的（　　）

A. B. C. D.

【题目】如图，矩形纸片，是的中点，是上一动点，沿折叠，点落在点处；延长交于点，连接.

（1）求证：≌；

（2）当时，将沿折叠，点落在线段上点处.

①求证：∽；

②如果，，求的长.

【题目】黄石市在创建国家级文明卫生城市中，绿化档次不断提升．某校计划购进A，B两种树木共100棵进行校园绿化升级，经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．

（1）求A种，B种树木每棵各多少元？

（2）因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．

【题目】如图1，已知抛物线()与轴交于、两点(在的右侧)，与轴的正半轴交于点，对称轴与轴交于点，作直线．

(1)求点、、的坐标：

(2)当以为圆心的圆与轴和直线都相切时，求抛物线的解析式：

(3)在(2)的条件下，如图2．是轴负半轴上的一点，过点作轴的平行线，与直线交于点，与抛物线交于点，连接，将沿翻折，的对应点为．在图2中探究：是否存在点，使得恰好落在轴上?若存在，请求出的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网