题目内容
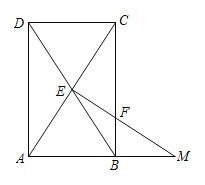
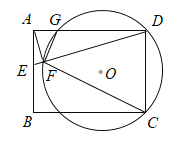
【题目】(问题情境)定义:如图1,点E在四边形ABCD的边CD上,若AE、BE将四边形ABCD分割成三个相似的三角形,则称点E为该四边形的相似点.

(1)若相似点在四边形ABCD的边CD上, 且AE、BE将四边形ABCD分割成三个正三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(2)若相似点在四边形ABCD的边CD上,且AE、BE将四边形ABCD分割成三个全等的等腰直角三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(3)(探索研究)
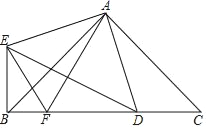
如图2,点E为四边形ABCD边上的相似点,且AE、BE将四边形ABCD分割成三个全等的三角形,已知∠ABC=90°,AD=AB=BC=2,求边CD的长.
(4)(问题解决)
如图3,在四边形ABCD中,AB∥CD,点E为四边形ABCD的边CD上的相似点,且AD=a,AB=b,BC=c(其中a≠c),此时边CD的长为多少?请用含a、b、c的代数式直接写出所有可能的结果.
【答案】(1)四边长度的比为1:1:1:2;(2)四边之比为1:1:![]() :2
:2![]() ;(3)CD=
;(3)CD=![]() ;(4)CD=
;(4)CD=![]()
【解析】
(1)根据相似点的定义以及分成三个正三角形得出这三个三角形全等,从而得出边之比;
(2)根据等腰直角三角形边之间的关系为![]() 设参数即可得出答案;
设参数即可得出答案;
(3)根据全等以及![]() 寻找出特殊角度的三角形再进行求解;
寻找出特殊角度的三角形再进行求解;
(4)根据![]() 和相似点的定义判断出四边形
和相似点的定义判断出四边形![]() 是平行四边形,从而得出
是平行四边形,从而得出![]() ,再根据对应边成比例计算
,再根据对应边成比例计算![]() ,从而得出答案.
,从而得出答案.
(1)∵![]() 均为正三角形,且三个三角形相似
均为正三角形,且三个三角形相似
∴这三个三角形全等
设![]()
∴则![]()
∴四边长度的比为![]()
(2)∵三个三角形为等腰直角三角形
∴设![]() ,则
,则![]()
∴四边之比为![]()
(3)过点A作AF⊥DE如图:

∵![]()
∴![]()
∴在直角三角形![]() 中:
中:![]()
在直角三角形![]() 中,
中,![]() ,
, ![]()
∴![]() =
=![]() +
+![]() +
+![]() =
=![]()
(4)∵![]()
根据相似点的含义可知,![]()
∴![]() ,
,![]() ,
,![]()
∵![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]()
∴![]()
∴![]()
∴![]()

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】为弘扬祖国优秀传统文化,加强优秀文化熏陶,提高学生的文化素养和道德素质,我县某校举行了“经典启迪人生,国学伴我成长”主题活动,学校统一印制独具本校特色的国学教育校本教材,通过课堂教学和课外活动相结合的方式进行国学教育,为了解学生学习成果,现随机抽取了部分同学的国学成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.调查结果扇形统计图.
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 50≤x<60 | 40 | 0.10 |
B | 60≤x<70 | 60 | c |
C | 70≤x<80 | a | 0.20 |
D | 80≤x<90 | 160 | 0.40 |
E | 90≤x<100 | 60 | 0.15 |
合计 | b | 1 |
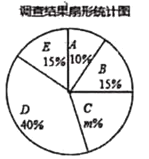
(1)根据以上信息解答问题:(1)统计表中a=________,b= ________,c=_______.
(2)扇形统计图中,m的值为________,“D”所对应的圆心角的度数是_______度;
(3)若参加国学教育的同学共有2000人,请你估计成绩在90分及以上的学生大约有多少人?