Question

【题目】（本小题满分10分）

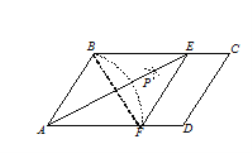
如图，在□ABCD中，以点A为圆心，AB长为半径画弧交AD于点F；再分别以点B、F为圆心，大于BF的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，则所得四边形ABEF是菱形．

（1）根据以上尺规作图的过程，求证四边形ABEF是菱形；

（2）若菱形ABEF的周长为16，AE＝4，求∠C的大小．

Answer 1

【答案】（1）详见解析；（2）60°.

【解析】

试题分析：（1）由作图过程可知，AB＝AF，AE平分∠BAD，即可得∠BAE＝∠EAF．再由四边形ABCD为平行四边形，可得BC∥AD，根据平行线的性质可得∠AEB＝∠EAF，所以∠BAE＝∠AEB，根据等腰三角形的性质可得AB＝BE，即可得BE＝AF，所以四边形ABEF为平行四边形，根据一组邻边相等的平行四边形是菱形即可判定四边形ABEF为菱形；（2）连接BF，已知四边形ABEF为菱形，根据菱形的性质可得BF与AE互相垂直平分，∠BAE＝∠FAE，OA＝AE＝．再由菱形ABEF的周长为16，可得AF＝4．所以cos∠OAF＝＝．即可得∠OAF＝30°，所以∠BAF＝60°．再由平行线的性质即可得∠C＝∠BAD＝60°．

试题解析：

（1）由作图过程可知，AB＝AF，AE平分∠BAD．∴∠BAE＝∠EAF．

∵四边形ABCD为平行四边形，∴BC∥AD．∴∠AEB＝∠EAF．

∴∠BAE＝∠AEB，∴AB＝BE．∴BE＝AF．∴四边形ABEF为平行四边形．

∴四边形ABEF为菱形．

（2）连接BF，

∵四边形ABEF为菱形，∴BF与AE互相垂直平分，∠BAE＝∠FAE．

∴OA＝AE＝．∵菱形ABEF的周长为16，∴AF＝4．

∴cos∠OAF＝＝．∴∠OAF＝30°，∴∠BAF＝60°．

∵四边形ABCD为平行四边形，∴∠C＝∠BAD＝60°．