Question

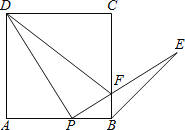
【题目】如图，E为边长为1的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任一点，PQ⊥BC于Q，PR⊥BE于R．有下列结论：①△PCQ∽△PER；②；③；④．其中正确的结论的个数是（　　）

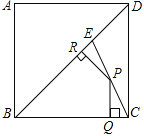
A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

①根据两角对应相等的两个三角形相似,即可证出;②作△DCE的边DC上的高EF,根据三角形的面积公式即可得出△DCE的面积;③解直角△CEF,即可求出∠DCE的正切值;④连接BP,利用面积法求解,PQ+PR的值等于C点到BE的距离,即正方形对角线的一半．

解:①∵BE＝BC,

∴∠QCP＝∠REP,

又∵∠PQC＝∠PRE＝90°,

∴△PCQ∽△PER,故正确;

②作△DCE的边DC上的高EF．

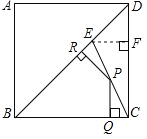
∵BE＝BC＝1,

∴DE＝BD﹣BE＝﹣1,

∵△DEF是等腰直角三角形,

∴EF＝DF＝DE＝,

∴S△DCE＝CDEF＝,故正确;

③在△CEF中,∠EFC＝90°,EF＝,

CF＝CD﹣DF＝1﹣＝,

∴tan∠DCE＝＝﹣1,故正确;

④连接BP,过C作CM⊥BD于M,

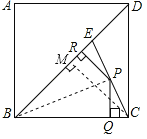
∵BC＝BE,

∴S△BCE＝S△BPE+S△BPC＝BC×PQ×+BE×PR×＝BC×（PQ+PR）×＝BE×CM×,∴PQ+PR＝CM,

∵BE＝BC＝1且正方形对角线BD＝,又BC＝CD,CM⊥BD,

∴为BD中点,又△BDC为直角三角形,

∴CM＝BD＝,

∴PQ+PR＝,故正确．

故选D．