Question

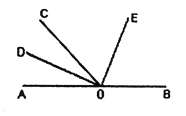
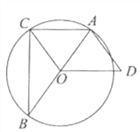
【题目】如图，已知△ABC内接于，AB是直径，OD∥AC，AD=OC.

(1)求证：四边形OCAD是平行四边形；

(2)填空：①当∠B= 时，四边形OCAD是菱形；

②当∠B= 时，AD与相切.

Answer 1

【答案】（1）证明见解析；（2）① 30°，② 45°

【解析】试题分析：（1）根据已知条件求得∠OAC=∠OCA，∠AOD=∠ADO，然后根据三角形内角和定理得出∠AOC=∠OAD，从而证得OC∥AD，即可证得结论；
（2）①若四边形OCAD是菱形，则OC=AC，从而证得OC=OA=AC，得出∠即可求得
②AD与相切，根据切线的性质得出根据AD∥OC，内错角相等得出从而求得

试题解析：(方法不唯一)

(1)∵OA=OC，AD=OC，

∴OA=AD，

∴∠OAC=∠OCA，∠AOD=∠ADO，

∵OD∥AC，

∴∠OAC=∠AOD，

∴∠OAC=∠OCA=∠AOD=∠ADO，

∴∠AOC=∠OAD，

∴OC∥AD，

∴四边形OCAD是平行四边形；

(2)①∵四边形OCAD是菱形，

∴OC=AC，

又∵OC=OA，

∴OC=OA=AC，

∴

∴

故答案为：

②∵AD与相切，

∴

∵AD∥OC，

∴

∴

故答案为：