ЬтФПФкШн
ЁОЬтФПЁПЮвУЧЙцЖЈЃКШ§НЧаЮШЮвтСНБпЕФЁАМЋЛЏжЕЁБЕШгкЕкШ§БпЩЯЕФжаЯпКЭетБпвЛАыЕФЦНЗНВюЃЎШчЭМ1ЃЌдкЁїABCжаЃЌAOЪЧBCБпЩЯЕФжаЯпЃЌABгыACЕФЁАМЋЛЏжЕЁБОЭЕШгкAO2ЉBO2ЕФжЕЃЌПЩМЧЮЊABЁїAC=AO2ЉBO2ЃЎ
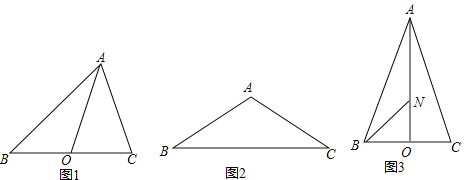
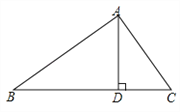
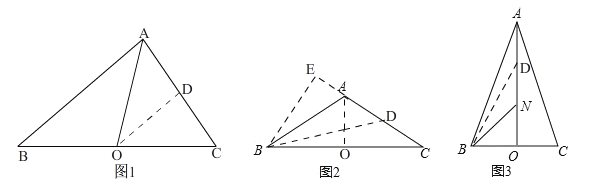
ЃЈ1ЃЉдкЭМ1жаЃЌШєЁЯBAC=90ЁуЃЌAB=8ЃЌAC=6ЃЌAOЪЧBCБпЩЯЕФжаЯпЃЌдђABЁїAC= ЃЌOCЁїOA= ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌAB=AC=4ЃЌЁЯBAC=120ЁуЃЌЧѓABЁїACЁЂBAЁїBCЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЁїABCжаЃЌAB=ACЃЌAOЪЧBCБпЩЯЕФжаЯпЃЌЕуNдкAOЩЯЃЌЧвON=![]() AOЃЎвбжЊABЁїAC=14ЃЌBNЁїBA=10ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
AOЃЎвбжЊABЁїAC=14ЃЌBNЁїBA=10ЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0ЃЌ7ЃЛЃЈ2ЃЉЉ8ЃЌ24ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
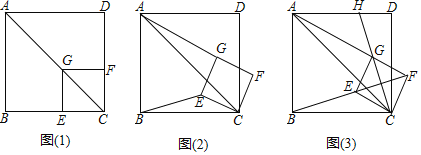
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйЯШИљОнЙДЙЩЖЈРэЧѓГіBC=10ЃЌдйРћгУжБНЧШ§НЧаЮЕФаджЪЕУГіOA=OB=OC=5ЃЌзюКѓРћгУаТЖЈвхМДПЩЕУГіНсТлЃЛ
ЂкдйгУЕШбќШ§НЧаЮЕФаджЪЧѓГіCD=3ЃЌдйРћгУЙДЙЩЖЈРэЧѓГіODЃЌзюКѓгУаТЖЈвхМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЂйЯШРћгУКЌ30ЁуЕФжБНЧШ§НЧаЮЕФаджЪЧѓГіAO=2ЃЌOB=![]() ЃЌдйгУаТЖЈвхМДПЩЕУГіНсТлЃЛ
ЃЌдйгУаТЖЈвхМДПЩЕУГіНсТлЃЛ
ЂкЯШЙЙдьжБНЧШ§НЧаЮЧѓГіBEЃЌAEЃЌдйгУЙДЙЩЖЈРэЧѓГіBDЃЌзюКѓгУаТЖЈвхМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШЙЙдьжБНЧШ§НЧаЮЃЌБэЪіГіOAЃЌBD2ЃЌзюКѓгУаТЖЈвхНЈСЂЗНГЬзщЧѓНтМДПЩЕУГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЂйЁпЁЯBAC=90ЁуЃЌAB=8ЃЌAC=6ЃЌЁрBC=10ЃЌ
ЁпЕуOЪЧBCЕФжаЕуЃЌЁрOA=OB=OC=![]() BC=5ЃЌЁрABЁїAC=AO2ЉBO2=25Љ25=0ЃЌ
BC=5ЃЌЁрABЁїAC=AO2ЉBO2=25Љ25=0ЃЌ
ЂкШчЭМ1ЃЌШЁACЕФжаЕуDЃЌСЌНгODЃЌЁрCD=![]() AC=3ЃЌ
AC=3ЃЌ
ЁпOA=OC=5ЃЌЁрODЁЭACЃЌ
дкRtЁїCODжаЃЌOD=![]() =4ЃЌЁрOCЁїOA=OD2ЉCD2=16Љ9=7ЃЌ
=4ЃЌЁрOCЁїOA=OD2ЉCD2=16Љ9=7ЃЌ
ЙЪД№АИЮЊЃК0ЃЌ7ЃЛ
ЃЈ2ЃЉЂйШчЭМ2ЃЌШЁBCЕФжаЕуDЃЌСЌНгAOЃЌЁпAB=ACЃЌЁрAOЁЭBCЃЌ
дкЁїABCжаЃЌAB=ACЃЌЁЯBAC=120ЁуЃЌЁрЁЯABC=30ЁуЃЌ
дкRtЁїAOBжаЃЌAB=4ЃЌЁЯABC=30ЁуЃЌЁрAO=2ЃЌOB=![]() ЃЌ
ЃЌ
ЁрABЁїAC=AO2ЉBO2=4Љ12=Љ8ЃЌ
ЂкШЁACЕФжаЕуDЃЌСЌНгBDЃЌЁрAD=CD=![]() AC=2ЃЌЙ§ЕуBзїBEЁЭACНЛCAЕФбгГЄЯпгкEЃЌдкRtЁїABEжаЃЌЁЯBAE=180ЁуЉЁЯBAC=60ЁуЃЌЁрЁЯABE=30ЁуЃЌ
AC=2ЃЌЙ§ЕуBзїBEЁЭACНЛCAЕФбгГЄЯпгкEЃЌдкRtЁїABEжаЃЌЁЯBAE=180ЁуЉЁЯBAC=60ЁуЃЌЁрЁЯABE=30ЁуЃЌ
ЁпAB=4ЃЌЁрAE=2ЃЌBE=![]() ЃЌЁрDE=AD+AE=4ЃЌ
ЃЌЁрDE=AD+AE=4ЃЌ
дкRtЁїBEDжаЃЌИљОнЙДЙЩЖЈРэЕУЃЌBD=![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЁрBAЁїBC=BD2ЉCD2=24ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЩшON=xЃЌOB=OC=yЃЌЁрBC=2yЃЌOA=3xЃЌ
ЁпABЁїAC=14ЃЌЁрOA2ЉOB2=14ЃЌЁр9x2Љy2=14ЂйЃЌ
ШЁANЕФжаЕуDЃЌСЌНгBDЃЌЁрAD=DB=![]() AN=
AN=![]() ЁС
ЁС![]() OA=ON=xЃЌЁрOD=ON+DN=2xЃЌ
OA=ON=xЃЌЁрOD=ON+DN=2xЃЌ
дкRtЁїBODжаЃЌBD2=OB2+OD2=y2+4x2ЃЌЁпBNЁїBA=10ЃЌ
ЁрBD2ЉDN2=10ЃЌЁрy2+4x2Љx2=10ЃЌЁр3x2+y2=10Ђк
СЊСЂЂйЂкЕУЃК 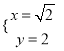 Лђ
Лђ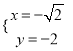 ЃЈЩсЃЉЃЌЁрBC=4ЃЌOA=
ЃЈЩсЃЉЃЌЁрBC=4ЃЌOA=![]() ЃЌЁрSЁїABC=
ЃЌЁрSЁїABC=![]() BCЁСAO=
BCЁСAO=![]() ЃЎ
ЃЎ

ЁОЬтФПЁПдкЫЎЙћЯњЪлЭњМОЃЌФГЫЎЙћЕъЙКНјвЛгХжЪЫЎЙћЃЌНјМлЮЊ20дЊ/ЧЇПЫЃЌЪлМлВЛЕЭгк20дЊ/ЧЇПЫЃЌЧвВЛГЌЙ§32дЊ/ЧЇПЫЃЌИљОнЯњЪлЧщПіЃЌЗЂЯжИУЫЎЙћвЛЬьЕФЯњЪлСПyЃЈЧЇПЫЃЉгыИУЬьЕФЪлМлxЃЈдЊ/ЧЇПЫЃЉТњзуШчЯТБэЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕЃЎ
ЯњЪлСПyЃЈЧЇПЫЃЉ | Ё | 34.8 | 32 | 29.6 | 28 | Ё |
ЪлМлxЃЈдЊ/ЧЇПЫЃЉ | Ё | 22.6 | 24 | 25.2 | 26 | Ё |
ЃЈ1ЃЉФГЬьетжжЫЎЙћЕФЪлМлЮЊ23.5дЊ/ЧЇПЫЃЌЧѓЕБЬьИУЫЎЙћЕФЯњЪлСПЃЎ
ЃЈ2ЃЉШчЙћФГЬьЯњЪлетжжЫЎЙћЛёРћ150дЊЃЌФЧУДИУЬьЫЎЙћЕФЪлМлЮЊЖрЩйдЊЃП