题目内容
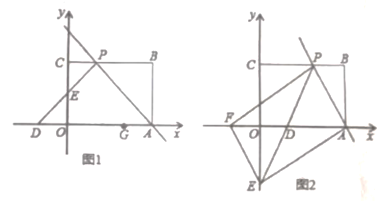
【题目】如图,△ABC是一块直角三角框,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角框内部,将圆形纸片沿着三角框的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,则圆心O运动的路径长为_____.

【答案】15+![]()
【解析】分析:添加如图所示辅助线,圆心O的运动路径长为![]() ,先求出
,先求出![]() 的三边长度,得出其周长,证四边形OEDO1,四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,四边形OECF为正方形,得出
的三边长度,得出其周长,证四边形OEDO1,四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,四边形OECF为正方形,得出![]() 从而知
从而知![]() 利用相似三角形的性质即可得出答案.
利用相似三角形的性质即可得出答案.
详解:如图,圆心O的运动路径长为![]() ,
,

过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB,垂足分别为点D. F.G,
过点O作OE⊥BC,垂足为点E,连接O2B,
过点O2作O2H⊥AB,O2I⊥AC,垂足分别为点H、I,
在Rt△ABC中, ![]()
∴
∴![]()
∵O1D⊥BC、O1G⊥AB,
∴D、G为切点,
∴BD=BG,
在Rt△O1BD和Rt△O1BG中,
∵![]()
∴△O1BD≌△O1BG(HL),
∴![]()
在Rt△O1BD中, ![]()
∴
∴![]()
∵O1D=OE=2,O1D⊥BC,OE⊥BC,
∴O1D∥OE,且O1D=OE,
∴四边形OEDO1为平行四边形,
∵![]()
∴四边形OEDO1为矩形,
同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,
又OE=OF,
∴四边形OECF为正方形,
∵![]()
∴![]()
又∵![]()
∴![]()
同理, ![]()
∴△OO1O2∽△CBA,
∴![]() 即
即![]()
∴![]() 即圆心O运动的路径长为
即圆心O运动的路径长为![]() .
.
故答案为: ![]()

【题目】某校举办了一次趣味数学党赛,满分100分,学生得分均为整数,这次竞赛中,甲、乙两组学生成绩如下(单位:分)
甲组:30,60,60,60,60,60,70,90,90,100
乙组:50,60,60,60,70,70,70,70,80,90.
组别 | 平均分 | 中位数 | 方差 |
甲组 | 68 | a | 376 |
乙组 | b | 70 |
(1)以生成绩统计分析表中a=_________分,b=_________分.
(2)小亮同学说:“这次赛我得了70分,在我们小组中属中游略偏上!”双察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由。
(3)计算乙组成的方差,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会进择哪一组?并说明理由。