题目内容
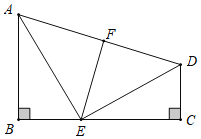
【题目】如图 ,已知B C=90 ,AEED,ABCE ,点F是AD的中点.说明EF与AD垂直的理由.
解:因为 AEED (已知),
所以AED=90 (垂直的意义).
因为AECBBAE ( ),
即AEDDECBBAE .
又因为B=90 (已知),
所以BAECED (等式性质).
在△ ABE 与△ ECD 中,
BC(已知),ABEC(已知),BAECED,
所以△ ABE≌△ECD ( ),
得 ( 全等三角形的对应边相等),
所以△AED 是等腰三角形.
因为 (已知),
所以 EFAD ( ).
【答案】见解析.
【解析】
证出∠BAE=∠CED,证明△ABE ≌△ECD,得出AE=DE,可知△AED是等腰三角形,由等腰三角形的三线合一性质即可得出结论.
因为AE ED(已知),
所以AED=90(垂直的意义),
因为AEC B BAE( 三角形的一个外角等于与它不相邻的两个内角的和),
即AED DEC B BAE,
又因为B=90(已知),
所以BAE CED(等式性质).
在△ABE与△ECD 中,
B C(已知),AB EC(已知),BAE CED,
所以△ABE≌△ECD(ASA).
得AE ED(全等三角形对应边相等).
所以△AED 是等腰三角形.
因为点F是AD的中点(已知),
所以EF AD(等腰三角形的三线合一).

练习册系列答案
相关题目
【题目】列方程解应用题
学校给七年级学生组织知识竞赛,共设20道题,各题的分值相同,每题必答.下表记录了5名学生的得分情况
参赛者 | 答对题数 | 答错题数 | 得分 |
小明 | 10 | 10 | 40 |
小红 | 19 | 1 | 94 |
小刚 | 20 | 0 | 100 |
小强 | 18 | 2 | 88 |
小丽 | 14 | 6 | 64 |
(1)参赛者小芳得76分,她答对了几道题?
(2)参赛者小花说她得了83分,你认为可能吗?为什么?





