题目内容
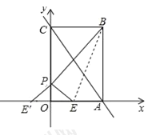
【题目】如图,把矩形![]() 放入平面直角坐标系
放入平面直角坐标系![]() 中,使
中,使![]() 分别落在
分别落在![]() 轴的正半轴上,其中
轴的正半轴上,其中![]() ,对角线
,对角线![]() 所在直线解析式为
所在直线解析式为![]() ,将矩形
,将矩形![]() 沿着
沿着![]() 折叠,使点
折叠,使点![]() 落在边
落在边![]() 上的
上的![]() 处.
处.

(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的长度;
的长度;
(3)点![]() 是
是![]() 轴上一动点,是否存在点
轴上一动点,是否存在点![]() 使得
使得![]() 的周长最小,若存在,请求出点
的周长最小,若存在,请求出点![]() 的坐标,如不存在,请说明理由.
的坐标,如不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,见解析.
,见解析.
【解析】
(1)根据点C的坐标确定b的值,利用待定系数法求出点A坐标即可解决问题;
(2)在Rt△BCD中,BC=6,BD=AB=10, CD=![]() =8, OD=10-8=2,设DE=AE=x,在Rt△DEO中,根据DE2=OD2+OE2,构建方程即可解决问题;
=8, OD=10-8=2,设DE=AE=x,在Rt△DEO中,根据DE2=OD2+OE2,构建方程即可解决问题;
(3)如图作点E关于y轴的对称点E′,连接BE′交y轴于P,此时△BPE的周长最小.利用待定系数法求出直线BE′的解析式即可解决问题;
解:![]() ,四边形
,四边形![]() 是矩形,
是矩形,
![]()
![]() ,代入
,代入![]() 得到
得到![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
令![]() ,得到
,得到
![]() .
.
![]() 在
在![]() 中,
中,![]()
![]() ,
,
![]()
设![]()
在![]() 中,
中, ![]()
![]()
![]()
![]()
![]() 如图作点
如图作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() ,此时
,此时![]() 的周长最小.
的周长最小.
![]()
![]()
设直线![]() 的解析式为
的解析式为![]() ,则有
,则有 ,解得:
,解得:
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]()

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目





