题目内容
【题目】如图1,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)若![]() 为等腰直角三角形.
为等腰直角三角形.
①求直线![]() 的函数解析式;
的函数解析式;
②在![]() 轴上另有一点
轴上另有一点![]() 的坐标为
的坐标为![]() ,请在直线
,请在直线![]() 和
和![]() 轴上分别找一点
轴上分别找一点![]() 、
、![]() ,使
,使![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
(2)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求直线
为顶点的四边形是平行四边形,求直线![]() 的解析式.
的解析式.
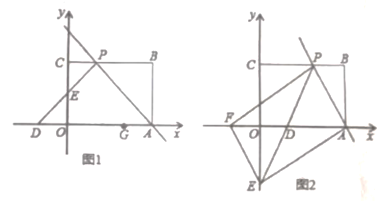
【答案】(1)①直线![]() 解析式
解析式![]() , ②N(0,
, ②N(0,![]() ),
),![]() 周长的最小值为
周长的最小值为![]() ;(2)
;(2)![]() .
.
【解析】
(1)①利用矩形的性质确定A、B、C点的坐标,再利用等腰三角的性质确定![]() ,所以
,所以![]() ,确定P点的坐标,再根据A点的坐标确定确定直线AP的函数表达式. ②作G点关于y轴对称点G'(-2,0),作点G关于直线AP对称点G'(3,1)
,确定P点的坐标,再根据A点的坐标确定确定直线AP的函数表达式. ②作G点关于y轴对称点G'(-2,0),作点G关于直线AP对称点G'(3,1)
连接G'G'交y轴于N,交直线AP于M,此时ΔGMN周长的最小.(2)过P作PM⊥AD于M,先根据等腰三角形三线合一的性质证明DM=MA ,再根据角角边定理证明ΔODE≌ΔMDP,根据全等三角形的性质求出点P、D的坐标,代入直线解析式得k=2,b=-2,所以直线PE的解析式为y=2x-2.
(1)①∵矩形![]() ,
,![]()
∴![]() ,
,
![]()
∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
设直线![]() 解析式
解析式![]() ,过点
,过点![]() ,点
,点![]()
∴![]() ∴
∴![]()
∴直线![]() 解析式
解析式![]()
②作![]() 点关于
点关于![]() 轴对称点
轴对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 对称点
对称点![]()
连接![]() 交
交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() ,此时
,此时![]() 周长的最小.
周长的最小.

∵![]()
∴直线![]() 解析式
解析式![]()
当![]() 时,
时,![]() ,∴
,∴![]()
∵![]()
∴![]() 周长的最小值为
周长的最小值为![]()
(2)如图:作![]() 于
于![]()

∵![]() ∴
∴![]() 且
且![]()
∴![]() ,且
,且![]() ∴
∴![]()
∵四边形![]() 是平行四边形 ∴
是平行四边形 ∴![]()
又∵![]()
∴![]()
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]()
设直线![]() 的解析式
的解析式![]()
![]() ∴
∴![]()
∴直线![]() 解析式
解析式![]()

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
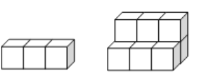
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)
【题目】为了了解某校学生的课外阅读情况,随机抽查了![]() 名学生周阅读用时数,结果如下表:
名学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 3 | 4 | 2 | 1 |
则关于这![]() 名学生周阅读所用时间,下列说法正确的是( )
名学生周阅读所用时间,下列说法正确的是( )
A. 中位数是![]() B. 众数是
B. 众数是![]() C. 平均数是
C. 平均数是![]() D. 方差是
D. 方差是![]()



