题目内容
【题目】如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=![]() BC,求线段PQ的长.
BC,求线段PQ的长.
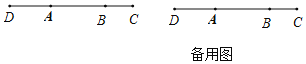
【答案】(1)9;(2)1或3.
【解析】
(1)利用AB=2BC计算出BC=2,则AC=6,再利用AC=2AD得到AD=3,然后计算AC+AD得到线段CD的长;
(2)利用线段中点的定义BQ=2,BP=1,讨论:当点P在B、C之间时,计算BP+BQ;当点P在A、B之间时,计算BQ﹣BP.
(1)∵AB=4,AB=2BC,
∴BC=2,
∴AC=AB+BC=6,
∵AC=2AD,
∴AD=3,
∴CD=AC+AD=6+3=9;
(2)∵Q为AB中点,
∴BQ=![]() AB=2,
AB=2,
∵BP=![]() BC,
BC,
∴BP=1,
当点P在B、C之间时,PQ=BP+BQ=2+1=3;
当点P在A、B之间时,PQ=BQ﹣BP=2﹣1=1.
即PQ的长为1或3.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目