��Ŀ����
����Ŀ��������Զ�Ǽ����������п��ij鿼��Ŀ֮һ��ijУ���꼶��1������2���������幺��ijƷ�Ƶ�������Զѵ��Ь�����˽ij��������������Ʒ��ѵ��Ь�Ĵ�������乺��ĵ���y��Ԫ/˫����һ���Թ��������x��˫��֮������ĺ�����ϵ��ͼ��ʾ��
��1����10��x��60ʱ����y����x�ĺ�������ʽ��
��2���ţ�1������2��������Ʒ��Ь��100˫������ij��ԭ��������ι�����һ�ι�����������25˫������60˫��
�������ι���Ь�ӹ�����9200Ԫ�����һ�εĹ���������
����ι滮���ι���ķ�����ʹ�����������٣����ٶ���Ԫ��
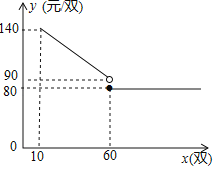
���𰸡���1��y��150��x�� ��2���ٵ�һ����������Ϊ30˫��40˫���ڵ�һ����26˫���ڶ�����74˫��ʡǮ������9144Ԫ��
��������
��1��������x˫��10��x��60����ÿ���ĵ��ۣ�140��������������10�������˿ɵ�y����x�ĺ�����ϵʽ��
��2�������һ������x˫����ڶ�������100��x��˫�����ݹ�������Ь��һ������9200Ԫ�г�������⼴�ɣ�������������ǣ���25��x��40ʱ����60��100��x��75����40��x��60ʱ����40��100��x��60��
�ڰ����εĻ������һ�ι����˫���ú�����ʾ������
�⣺��1������x˫��10��x��60��ʱ��y��140����x��10����150��x��
��y����x�ĺ�����ϵʽ��y��150��x��
��2�������һ������x˫����ڶ�������100��x��˫��
��25��x��40ʱ����60��100��x��75����x��150��x��+80��100��x����9200��
���x1��30��x2��40��
��40��x��60ʱ����40��100��x��60��
��x��150��x��+��100��x��[150����100��x��]��9200��
���x��30��x��70����40��x��60�������⣻
�𣺵�һ����������Ϊ30˫��40˫��
�����һ�ι���x˫����ڶ��ι���100��x��˫�������λ���wԪ��
��25��x��40ʱw��x��150��x��+80��100��x��������x��35��2+9225��
��x��26ʱ��w����Сֵ����СֵΪ9144Ԫ��
��40��x��60ʱ��
w��x��150��x��+��100��x��[150����100��x��]����2��x��50��2+10000��
��x��41��59ʱ��w����Сֵ����СֵΪ9838Ԫ��
������������һ����26˫���ڶ�����74˫��ʡǮ������9144Ԫ��

 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�����Ŀ��ij��ѧ����ҵ�Ŷ�ץס�̻�������һ���ɹ���װ��Ӫ�����������С��װ����ۣ�ÿ���ɱ�3Ԫ�������ڼ䷢��ÿ���������![]() ����
����![]() �����۵���
�����۵���![]() ��Ԫ
��Ԫ![]() ֮������һ�κ�����ϵ���������������ʾ������3.5��x��5.5������ÿ�컹��֧�������������80Ԫ��
֮������һ�κ�����ϵ���������������ʾ������3.5��x��5.5������ÿ�컹��֧�������������80Ԫ��
���۵��� | 3.5 | 5.5 |
������ | 280 | 120 |
��1�������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2����ÿ�������Ϊ![]() Ԫ�������۵��۶�Ϊ����Ԫʱ��ÿ������������������Ƕ���Ԫ��
Ԫ�������۵��۶�Ϊ����Ԫʱ��ÿ������������������Ƕ���Ԫ��