题目内容
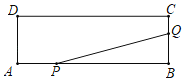
【题目】如图,矩形ABCD的两边长AB=16cm,AD=4cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动设运动时间为x(秒),设△BPQ的面积为ycm2.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)当△BPQ面积有最大值时,求x的值.
【答案】(1)y=﹣x2+8x(0<x≤4);(2)△BPQ面积有最大值时,x的值为4.
【解析】
(1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;
(2)把函数关系式整理成顶点式,然后根据二次函数的最值解答.
解:(1)∵S△PBQ=![]() PBBQ,PB=AB﹣AP=16﹣2x,BQ=x,
PBBQ,PB=AB﹣AP=16﹣2x,BQ=x,
∴y=![]() (16﹣2x)x,即y=﹣x2+8x(0<x≤4);
(16﹣2x)x,即y=﹣x2+8x(0<x≤4);
(2)∵y=﹣x2+8x=﹣(x﹣4)2+16,
∴当x=4时,y有最大值,
即△BPQ面积有最大值时,x的值为4.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目