题目内容
如图,矩形ABCD中,P是线段AD上一动点,O为BD中点,PO的延长线交BC于Q。
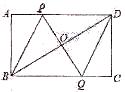
(1)求证:四边形PDQB为平行四边形;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向D运动(不与D重合)。设点P运动时间为t秒,请用t表示PD的长,并求t为何值时,四边形PBQD是菱形。

(1)求证:四边形PDQB为平行四边形;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向D运动(不与D重合)。设点P运动时间为t秒,请用t表示PD的长,并求t为何值时,四边形PBQD是菱形。
(1)先根据矩形的性质可得∠PDO=∠QBO,再结合对顶角相等O为BD中点,即可根据“AAS”证得△POD △QOB,则可得PO=OQ,从而证得结论;(2)
△QOB,则可得PO=OQ,从而证得结论;(2)
 △QOB,则可得PO=OQ,从而证得结论;(2)
△QOB,则可得PO=OQ,从而证得结论;(2)
试题分析:(1)先根据矩形的性质可得∠PDO=∠QBO,再结合对顶角相等O为BD中点,即可根据“AAS”证得△POD
 △QOB,则可得PO=OQ,从而证得结论;
△QOB,则可得PO=OQ,从而证得结论;(2)由PB=PD=8-t,在Rt△PAB中,根据勾股定理结合菱形的判定即可求得结果.
(1)在矩形ABCD中,AD∥BC
∴∠PDO=∠QBO,又∠POD=∠QOB
∵ O为BD中点,∴BO=DO
∴△POD
 △QOB(AAS)
△QOB(AAS)∴PO=OQ,又BO=OD
∴四边形PDQB为平行四边形;
(2)PD=8-t,在平行四边形PBQD中,当PB=PD时,平行四边形PBQD为菱形
∴PB=PD=8-t
在Rt△PAB中,

解得:

答:当
 时,四边形PBQD为菱形.
时,四边形PBQD为菱形.点评:本题知识点多,综合性强,难度较大,需要同学们熟练掌握特殊四边形的判定和性质.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

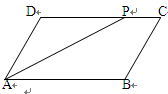

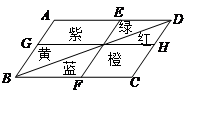
 ,它的周长是
,它的周长是 ,则它的中位线长为 ㎝.
,则它的中位线长为 ㎝. 中,点
中,点 在边
在边 上,
上, 为等边三角形,且点
为等边三角形,且点 与点
与点 的两侧,点
的两侧,点 在
在 上(不与
上(不与 重合)且
重合)且 ,
, 与
与 分别相交于点
分别相交于点 .
.
 是平行四边形
是平行四边形