题目内容
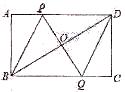
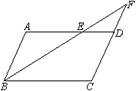
如图,在等边 中,点
中,点 在边
在边 上,
上, 为等边三角形,且点
为等边三角形,且点 与点
与点 在直线
在直线 的两侧,点
的两侧,点 在
在 上(不与
上(不与 重合)且
重合)且 ,
, 与
与 分别相交于点
分别相交于点 .
.

求证:四边形 是平行四边形
是平行四边形
 中,点
中,点 在边
在边 上,
上, 为等边三角形,且点
为等边三角形,且点 与点
与点 在直线
在直线 的两侧,点
的两侧,点 在
在 上(不与
上(不与 重合)且
重合)且 ,
, 与
与 分别相交于点
分别相交于点 .
.
求证:四边形
 是平行四边形
是平行四边形由 、
、 均为等边三角形可得
均为等边三角形可得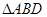 ≌
≌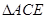 ,可得∠B=∠ACE=60°,则可得到
,可得∠B=∠ACE=60°,则可得到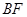 //
//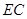 ,再由
,再由 可得
可得 //
// ,即可证得结论.
,即可证得结论.
 、
、 均为等边三角形可得
均为等边三角形可得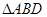 ≌
≌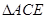 ,可得∠B=∠ACE=60°,则可得到
,可得∠B=∠ACE=60°,则可得到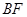 //
//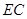 ,再由
,再由 可得
可得 //
// ,即可证得结论.
,即可证得结论.试题分析:∵
 、
、 均为等边三角形
均为等边三角形∴AB=AC,AD=AE,∠BAC=∠DAE=60°
∴∠BAD=∠CAE
∴
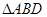 ≌
≌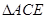
∴∠B=∠ACE=60°
∴∠BAC=∠ACE=60°
∴
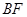 //
//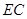
∵

∴
 //
//
∴四边形
 为平行四边形.
为平行四边形.点评:解答本题的关键是熟练掌握等边三角形的三条边相等,三个角均为60°;两组对边分别平行的四边形是平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则梯形ABCD的面积为( )
,则梯形ABCD的面积为( )
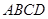 中,
中,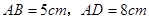 ,
,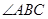 的平分线交
的平分线交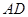 于点
于点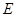 ,交
,交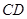 的延长线于点
的延长线于点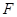 ,那么
,那么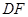 =
= 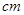
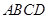 的两条对角线相交于点
的两条对角线相交于点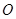 ,
,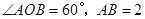 ,则矩形的边长
,则矩形的边长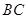 的长是( )
的长是( )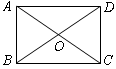
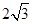
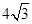
 两条对角线
两条对角线 相交于点
相交于点 ,∠
,∠ =60°,
=60°, =4,则
=4,则 的长是 .
的长是 .