题目内容
如图1,正方形ABCD中,点E、F分别在边DC、AD上,且AE⊥BF于G.

(1)求证:BF=AE;
(2)如图2,当点E在DC延长线上,点F在AD延长线上时,(1)中结论是否成立(直接写结论);
(3)在图2中,若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,且AF:AD=4:3,求S四边形MNPQ: S正方形ABCD

(1)求证:BF=AE;
(2)如图2,当点E在DC延长线上,点F在AD延长线上时,(1)中结论是否成立(直接写结论);
(3)在图2中,若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,且AF:AD=4:3,求S四边形MNPQ: S正方形ABCD
(1)∵正方形ABCD
∴AD=AB,∠ADC=∠DAB=90°
∴∠DAE+∠ABG=90°
∵AE⊥BF
∴∠ABG+∠GAB=90°
∴∠DAE=∠ABG
∴△ADE≌△BAF
∴BF=AE;
(2)结论成立;
(3)25:36
∴AD=AB,∠ADC=∠DAB=90°
∴∠DAE+∠ABG=90°
∵AE⊥BF
∴∠ABG+∠GAB=90°
∴∠DAE=∠ABG
∴△ADE≌△BAF
∴BF=AE;
(2)结论成立;
(3)25:36
试题分析:(1)根据正方形的性质及同角的余角相等即可证得△ADE≌△BAF,问题得证;
(2)证法同(1);
(3)先根据三角形的中位线定理证得MNPQ为正方形,再舍AD=3a,则BF=5a,MQ=
 ,再根据正方形的面积公式即可得到结果.
,再根据正方形的面积公式即可得到结果.(1)∵正方形ABCD
∴AD=AB,∠ADC=∠DAB=90°
∴∠DAE+∠ABG=90°
∵AE⊥BF
∴∠ABG+∠GAB=90°
∴∠DAE=∠ABG
∴△ADE≌△BAF
∴BF=AE;
(2)结论成立;
(3)∵点M、N分别为四边形AFEB四条边AF、EF的中点,
∴MN∥AE且MN=
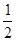 AE,
AE,同理可证:MQ∥BF且MQ=
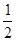 BF,PQ∥AE且PQ=
BF,PQ∥AE且PQ=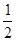 AE,NP∥BF且NP=
AE,NP∥BF且NP=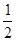 BF
BF∵AE=BF
∴MN=MQ=PQ=NP
∴四边形MNPQ是菱形
∵AE⊥BF
∴∠MQP=90°
∴四边形MNPQ是正方形
设AD=3a,则BF=5a
∴MQ=

∴S四边形MNPQ:S正ABCD=MQ2:AD2=(
 )2 :(3a)2=25:36.
)2 :(3a)2=25:36.点评:解答本题的关键是熟练掌握三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.

练习册系列答案
相关题目

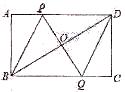
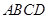 的两条对角线相交于点
的两条对角线相交于点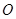 ,
,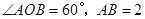 ,则矩形的边长
,则矩形的边长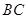 的长是( )
的长是( )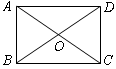
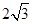
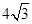
 在同一条直线上,
在同一条直线上, ,
, .
.
 .
.
 两条对角线
两条对角线 相交于点
相交于点 ,∠
,∠ =60°,
=60°, =4,则
=4,则 的长是 .
的长是 .