题目内容
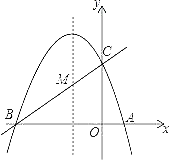
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴围成的
轴围成的![]() 的面积为
的面积为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 坐标并判断
坐标并判断![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的面积为
的面积为![]() ,求
,求![]() 点坐标.
点坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;直角三角形;(3)
;直角三角形;(3)![]() 或
或![]()
【解析】
(1)根据待定系数法即可求得;
(2)根据△BOC的面积求得C的坐标,然后根据勾股定理求得AC,AB、BC的长,根据勾股定理的逆定理即可判定△ABC是直角三角形;
(3)设P(x,0),则AP=|x+4|,根据三角形面积公式即可得到![]() ,解得即可.
,解得即可.
(1)设直线l1的解析式为y=kx+b,
∵直线l1,与x轴交于点A(-4,0),与直线l2相交于点B(0,3)
∴![]()
解得![]()
∴直线l1的解析式为![]()
故答案为:![]()
(2)设C(m,0),![]() ,
,
∵△BOC的面积为![]()
∴![]()
即![]()
解得m=![]()
∴C(![]() ,0),
,0),
∴AC=4+![]() =
=![]()
则AC2=![]()
∵AB2=32+42=25,BC2=(![]() )2+32=
)2+32=![]()
∴AB2+BC2=25+![]() =
=![]()
∴AB2+BC2=AC2,
∴△ABC是直角三角形;
故答案为:直角三角形,理由见解析
(3)设P(x,0),则AP=|x+4|,
∵△BAP的面积为9,![]() APOB=9,即
APOB=9,即
![]() |x-4|×3=9,
|x-4|×3=9,
解得x1=2,x2=-10,
∴P点的坐标为(2,0)或(-10,0)
故答案为: (2,0)或(-10,0)

练习册系列答案
相关题目