题目内容
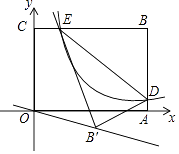
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y= ![]() (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE= ![]() ,则BN的长为 .
,则BN的长为 . 
【答案】3
【解析】解:∵S矩形OABC=32,
∴ABBC=32,
∵矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,
∴AB=DE,OD=OA,
在Rt△ODE中,tan∠DOE= ![]() =
= ![]() ,即OD=2DE,
,即OD=2DE,
∴DE2DE=32,解得DE=4,
∴AB=4,OA=8,
在Rt△OCM中,∵tan∠COM= ![]() =
= ![]() ,
,
而OC=AB=4,
∴MC=2,
∴M(﹣2,4),
把M(﹣2,4)代入y= ![]() 得k=﹣2×4=﹣8,
得k=﹣2×4=﹣8,
∴反比例函数解析式为y=﹣ ![]() ,
,
当x=﹣8时,y=﹣ ![]() =1,则N(﹣8,1),
=1,则N(﹣8,1),
∴BN=4﹣1=3.
所以答案是3.
【考点精析】解答此题的关键在于理解锐角三角函数的定义的相关知识,掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目