题目内容
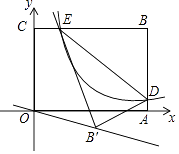
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( )

A.4B.3C.2D.1
【答案】B
【解析】
①利用HL证明可得;
②设AG=x,在△GBE中,利用勾股定理可得到关于x的方程,解得x的值,从而得出GF、GB的值;
③△GDF是直角三角形,直接按照面积公式求解即可;
④先求解出Rt△GBE的面积,△EBF的面积=△GBE的面积×![]() .
.
①∵△EDF是△EDC翻折得到,∴△EDF≌△EDC
∴DF=CD=AD=12,∠EFD=∠ECD=90°=∠GAD
∵GD=GD
∴△FGD≌△AGD,①正确
②设AG=x,则GF=x,GB=12-x
∵BE=EC,∴BE=EC=FE=6
∴在Rt△GBE中,![]() ,即:
,即:![]()
解得:x=4,∴AG=GF=4,BG=8,②正确
③![]() ,③错误
,③错误
④![]()
∴![]() ,④正确
,④正确
故选:B

练习册系列答案
相关题目