题目内容
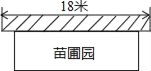
【题目】晨光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围;
(2)设这个苗圃园的面积为S,求S与x之间的函数关系.
【答案】(1)y=30﹣2x,(6≤x<15);(2)S=﹣2(x﹣7.5)2+112.5.
【解析】
(1)由总长度垂直于墙的两边的长度=平行于墙的这边的长度,根据墙的长度就可以求出![]() 的取值范围;
的取值范围;
(2)由长方形的面积公式建立二次函数即可.
解:(1)y=30﹣2x,(6≤x<15);
(2)设矩形苗圃的面积为S
S=xy=x(30﹣2x)=﹣2(x﹣7.5)2+112.5.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c(a≠0),该函数y与自变量x的部分对应值如下表:
x | … | 1 | 2 | 3 | … |
y | … | 0 | ﹣1 | 0 | … |
(1)求该二次函数的表达式;
(2)不等式ax2+bx+c>0的解集为 ;
不等式ax2+bx+c<3的解集为 .