题目内容
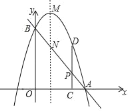
【题目】如图,已知直线y=﹣x+4分别交x轴、y轴于点A、B,抛物线过y=ax2+bx+c经过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣![]() x2+x+4,设其顶点为M,其对称轴交AB于点N.
x2+x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为2时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形是直角三角形?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.

【答案】(1)① M(1,![]() ),N(1,3); ②见解析;(2)见解析.
),N(1,3); ②见解析;(2)见解析.
【解析】
(1)①把二次函数表达式化为顶点式表达式,即可求解;
②不存在.理由如下:设点P 的坐标为(m,-m+4),则D(m,-![]() m2+m+4),PD=-
m2+m+4),PD=-![]() m2+m+4-(-m+4)=-
m2+m+4-(-m+4)=-![]() m2+2m,当四边形MNPD为平行四边形,则:
m2+2m,当四边形MNPD为平行四边形,则:![]() m2+2m=
m2+2m=![]() ,解得:m=1,则:点P(3,1),由N(1,3),则:PN=
,解得:m=1,则:点P(3,1),由N(1,3),则:PN=![]() ≠MN,即可求解;
≠MN,即可求解;
(2)分∠BDP=90°或∠PBD=90°两种情况,求解即可.
解:(1)①y=﹣![]() x2+x+4=﹣
x2+x+4=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴顶点M的坐标为(1,![]() ),
),
当x=1时,y=﹣1+4=3,
∴点N的坐标为(1,3);
②不存在.理由如下:
MN=![]() ﹣3=
﹣3=![]() ,
,
设点P 的坐标为(m,﹣m+4),则D(m,﹣![]() m2+m+4),
m2+m+4),
PD=﹣![]() m2+m+4﹣(﹣m+4)=﹣
m2+m+4﹣(﹣m+4)=﹣![]() m2+2m,
m2+2m,
∵PD∥MN.
∴当PD=MN时,四边形MNPD为平行四边形,
即﹣![]() m2+2m=
m2+2m=![]() ,解得:m=1或3(m=1舍去),
,解得:m=1或3(m=1舍去),
∴点P(3,1),由N(1,3),
∴PN=![]() ≠MN,
≠MN,
∴平行四边形MNPD不是菱形,
即:不存在点P,使四边形MNPD为菱形;
(2)①当∠BDP=90°时,点P(2,2),则四边形BOCD为矩形,
∴D(2,4),又A(4,0),B(0,4),
∴抛物线的表达式为:y=﹣![]() x2+x+4;
x2+x+4;
②当∠PBD=90°时,△PBD为等腰直角三角形,
则PD=2xP=4,
∴D(2,6),又A(4,0),B(0,4),
把A、B、D坐标代入二次函数表达式得: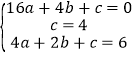 ,解得:
,解得: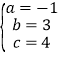 ,
,
故:二次函数表达式为:y=﹣x2+3x+4.

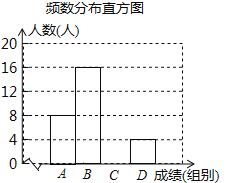
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .