Question

【题目】如图，广场上一个立体雕塑由两部分组成，底座是一个正方体，正上方是一个球体，且正方体的高度和球的高度相等．当阳光与地面的夹角成60°时，整个雕塑在地面上的影子AB长2米，求这个雕塑的高度．（结果精确到百分位，参考数据：≈1.73）

Answer 1

【答案】雕塑的高度为4.24米．

【解析】

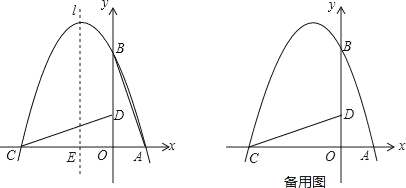
先过D作DF⊥AB于F，过O作OG⊥AB于G，过O作DF的垂线，交DF于H，交⊙O于E，则AE为⊙O的切线，延长AE交BD于C，设⊙O的半径为r，则OG= 3r=HF=AE，OD=r，根据∠ACB=30°，∠DOE=30°，得到Rt△ODH中，DH=OD=r，DF=r+3r，进而得出CE=CD=AC-AE=2-3r，再根据AC∥DF，得出，进而求得r≈1.06，据此可得这个雕塑的高度．

如图所示，设D为光线与⊙O的切点，过D作DF⊥AB于F，过O作OG⊥AB于G，

过O作DF的垂线，交DF于H，交⊙O于E，

则AE为⊙O的切线，延长AE交BD于C，

设⊙O的半径为r，则OG＝3r＝HF＝AE，OD＝r，

∵∠ABD＝60°，

∴∠ACB＝30°，∠DOE＝30°，

∴Rt△ODH中，DH＝OD＝r，

∴DF＝r+3r，

又∵Rt△ABC中，AB＝2，

∴AC＝2，BC＝4，

∴CE＝CD＝AC﹣AE＝2﹣3r，

∵AC∥DF，

∴，即，

解得r≈1.06，

∴雕塑的高度为4r＝4×1.06＝4.24米．