题目内容
【题目】在△ABC中,∠ACB=45°,点D为射线BC上一动点(与点B、C不重合),连接AD,以AD为一边在AD一侧作正方形ADEF(如图1).
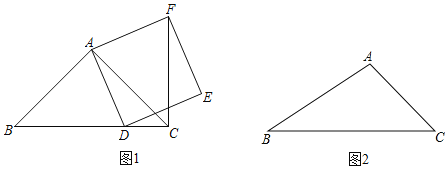
(1)如果AB=AC,且点D在线段BC上运动,证明:CF⊥BD;
(2)如果AB≠AC,且点D在线段BC的延长线上运动,请在图2中画出相应的示意图,此时(1)中的结论是否成立?请说明理由;
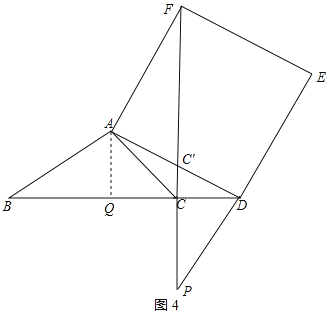
(3)设正方形ADEF的边DE所在直线与直线CF相交于点P,若AC=4,CD=2,求线段CP的长.
【答案】(1)见解析;(2)AB≠AC时,CF⊥BD的结论成立.理由见解析;(3)线段CP的长为2﹣![]() 或2+
或2+![]() .
.
【解析】
(1)证出∠BAC=∠DAF=90°,得出∠BAD=∠CAF;可证△DAB≌△FAC(SAS),得∠ACF=∠ABD=45°,得出∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.
(2)过点A作AG⊥AC交BC于点G,可得出AC=AG,易证△GAD≌△CAF(SAS),得出∠ACF=∠AGD=45°,∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.
(3)分两种情况去解答.①点D在线段BC上运动,求出AQ=CQ=4.即DQ=4﹣2=2,易证△AQD∽△DCP,得出对应边成比例,即可得出CP=![]() ;②点D在线段BC延长线上运动时,同理得出CP=
;②点D在线段BC延长线上运动时,同理得出CP=![]() .
.
(1)证明:∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∵AB=AC,∠BAC=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,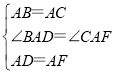 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°
∵AB=AC,∠BAC=90°,
∴∠ACB=∠ABD=45°
∴∠BCF=∠ACB+∠ACF=90°,
∴CF⊥BD;
(2)解:如图2所示:AB≠AC时,CF⊥BD的结论成立.理由如下:
过点A作GA⊥AC交BC于点G,
则∠GAD=∠CAF=90°+∠CAD,
∵∠ACB=45°,
∴∠AGD=45°,
∴AC=AG,
在△GAD和△CAF中,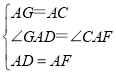 ,
,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGD=45°,
∴∠BCF=∠ACB+∠ACF=90°,
∴CF⊥BD;
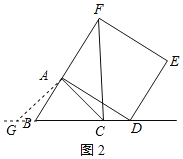
(3)解:过点A作AQ⊥BC交CB的延长线于点Q,
①点D在线段BC上运动时,如图3所示:
∵∠BCA=45°,
∴△ACQ是等腰直角三角形,
∵AC=4
∴AQ=CQ=![]() AC=
AC=![]() .
.
∴DQ=CQ﹣CD=![]() ﹣2,
﹣2,
∵AQ⊥BC,∠ADE=90°,
∴∠DAQ+∠ADQ=∠ADQ+∠PDC=90°,
∴∠DAQ=∠PDC,
∵∠AQD=∠DCP=90°,
∴△DCP∽△AQD,
∴![]() ,即
,即![]() ,
,
解得:CP=2﹣![]() ;
;
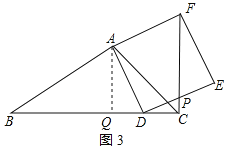
②点D在线段BC延长线上运动时,如图4所示:
∵∠BCA=45°,
∴AQ=CQ=![]() ,
,
∴DQ=AQ+CD=![]() +2.
+2.
∵AQ⊥BC于Q,
∴∠Q=∠FAD=90°,
∵∠C′AF=∠C′CD=90°,∠AC′F=∠CC′D,
∴∠ADQ=∠AFC′,
则△AQD∽△AC′F.
∴CF⊥BD,
∴△AQD∽△DCP,
∴![]() ,即
,即![]() ,
,
解得:CP=![]() ,
,
综上所述,线段CP的长为![]() 或
或![]() .
.

 字词句篇与同步作文达标系列答案
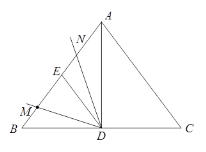
字词句篇与同步作文达标系列答案【题目】如图,在![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 为
为![]() 的中点,点E为AB的中点.点
的中点,点E为AB的中点.点![]() 为AB边上一动点,从点B出发,运动到点A停止,将射线DM绕点
为AB边上一动点,从点B出发,运动到点A停止,将射线DM绕点![]() 顺时针旋转
顺时针旋转![]() 度(其中
度(其中![]() ),得到射线DN,DN与边AB或AC交于点N.设
),得到射线DN,DN与边AB或AC交于点N.设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() cm,
cm,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() cm.
cm.
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小涛的探究过程,请补充完整.
(1)列表:按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值:
的几组对应值:
x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
请你通过测量或计算,补全表格;
(2)描点、连线:在平面直角坐标系![]() 中,描出补全后的表格中各组数值所对应的点
中,描出补全后的表格中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象.
的图象.
(3)结合函数图象,解决问题:当![]() 时,
时,![]() 的长度大约是 cm.(结果保留一位小数)
的长度大约是 cm.(结果保留一位小数)