题目内容
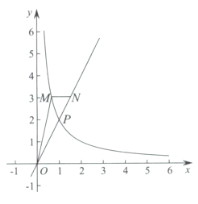
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
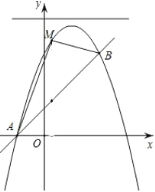
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】⑴![]() ;⑵当
;⑵当![]() ,
,![]() □MANB=
□MANB=![]() △
△![]() =
=![]() ,此时
,此时![]() ;⑶存在. 当
;⑶存在. 当![]() 时,无论
时,无论![]() 取任何实数,均有
取任何实数,均有![]() . 理由见解析.
. 理由见解析.
【解析】
(1)利用待定系数法,将A,B的坐标代入y=ax2+2x+c即可求得二次函数的解析式;
(2)过点M作MH⊥x轴于H,交直线AB于K,求出直线AB的解析式,设点M(a,-a2+2a+3),则K(a,a+1),利用函数思想求出MK的最大值,再求出△AMB面积的最大值,可推出此时平行四边形MANB的面积S及点M的坐标;
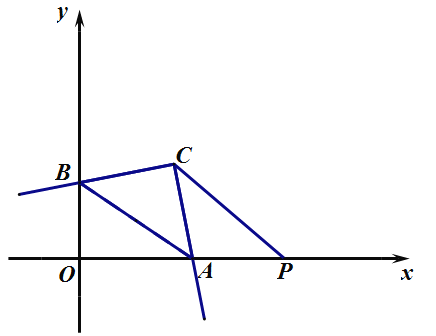
(3)如图2,分别过点B,C作直线y=![]() 的垂线,垂足为N,H,设抛物线对称轴上存在点F,使抛物线C上任意一点P到点F的距离等于到直线y=
的垂线,垂足为N,H,设抛物线对称轴上存在点F,使抛物线C上任意一点P到点F的距离等于到直线y=![]() 的距离,其中F(1,a),连接BF,CF,则可根据BF=BN,CF=CN两组等量关系列出关于a的方程组,解方程组即可.
的距离,其中F(1,a),连接BF,CF,则可根据BF=BN,CF=CN两组等量关系列出关于a的方程组,解方程组即可.
(1)由题意把点(-1,0)、(2,3)代入y=ax2+2x+c,
得,![]() ,
,
解得a=-1,c=3,
∴此抛物线C函数表达式为:y=-x2+2x+3;
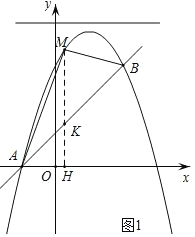
(2)如图1,过点M作MH⊥x轴于H,交直线AB于K,
将点(-1,0)、(2,3)代入y=kx+b中,
得,![]() ,
,
解得,k=1,b=1,
∴yAB=x+1,
设点M(a,-a2+2a+3),则K(a,a+1),
则MK=-a2+2a+3-(a+1)
=-(a-![]() )2+
)2+![]() ,
,
根据二次函数的性质可知,当a=![]() 时,MK有最大长度
时,MK有最大长度![]() ,
,
∴S△AMB最大=S△AMK+S△BMK
=![]() MKAH+
MKAH+![]() MK(xB-xH)
MK(xB-xH)
=![]() MK(xB-xA)
MK(xB-xA)
=![]() ×
×![]() ×3
×3
=![]() ,
,
∴以MA、MB为相邻的两边作平行四边形MANB,当平行四边形MANB的面积最大时,
S最大=2S△AMB最大=2×![]() =
=![]() ,M(
,M(![]() ,
,![]() );
);
(3)存在点F,
∵y=-x2+2x+3
=-(x-1)2+4,
∴对称轴为直线x=1,
当y=0时,x1=-1,x2=3,
∴抛物线与点x轴正半轴交于点C(3,0),
如图2,分别过点B,C作直线y=![]() 的垂线,垂足为N,H,
的垂线,垂足为N,H,
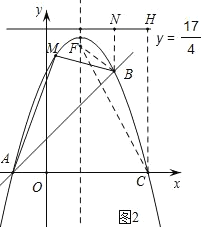
抛物线对称轴上存在点F,使抛物线C上任意一点P到点F的距离等于到直线y=![]() 的距离,设F(1,a),连接BF,CF,
的距离,设F(1,a),连接BF,CF,
则BF=BN=![]() -3=
-3=![]() ,CF=CH=
,CF=CH=![]() ,
,
由题意可列: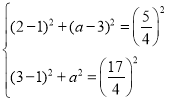 ,
,
解得,a=![]() ,
,
∴F(1,![]() ).
).