题目内容
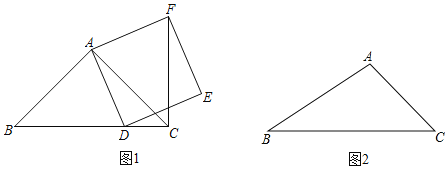
【题目】如图,在![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 为
为![]() 的中点,点E为AB的中点.点
的中点,点E为AB的中点.点![]() 为AB边上一动点,从点B出发,运动到点A停止,将射线DM绕点
为AB边上一动点,从点B出发,运动到点A停止,将射线DM绕点![]() 顺时针旋转
顺时针旋转![]() 度(其中
度(其中![]() ),得到射线DN,DN与边AB或AC交于点N.设
),得到射线DN,DN与边AB或AC交于点N.设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() cm,
cm,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() cm.
cm.
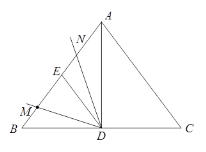
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小涛的探究过程,请补充完整.
(1)列表:按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值:
的几组对应值:
x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
请你通过测量或计算,补全表格;
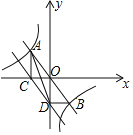
(2)描点、连线:在平面直角坐标系![]() 中,描出补全后的表格中各组数值所对应的点
中,描出补全后的表格中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象.
的图象.
(3)结合函数图象,解决问题:当![]() 时,
时,![]() 的长度大约是 cm.(结果保留一位小数)
的长度大约是 cm.(结果保留一位小数)
【答案】(1)3.2;(2)详见解析;(3)1.7,1.9,4.7
【解析】
(1)证明∠BMD=90°,则y=MN=MDtanβ=(DBsinβ)tanβ=2.4×![]() =3.2;
=3.2;
(2)描点、连线得函数图象;
(3)当MN=BD时,即y=3,从图象看x的值即可.
解:(1)x=BM=1.8,
因为AB=AC=5,BC=6,D为BC的中点,
∴BD=DC=3,AD⊥BC.
∴cos∠B=![]() ,tan∠B=
,tan∠B=![]() .
.
在△MBD中,BD=3,设cosB=cosβ,tanβ=![]() ,
,
过点M作MH⊥BD于点H,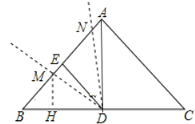
则BH=BMcosβ=1.8×![]() =1.08,同理MH=1.44,
=1.08,同理MH=1.44,
HD=BD-BH=3-1.08=1.92,
MD=![]() =2.4,
=2.4,
则BD2=BM2+MD2,
故∠BMD=90°,
在直角三角形ABD中,E是AB的中点,
∴BE=ED.
∴∠B=∠BDE.
又∵∠B=∠MDN.
∴∠MDN=∠B=β.
则y=MN=MDtanβ =2.4×![]() =3.2,
=3.2,
补全的表格数据如下:
x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 3.2 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
(2)描点、连线得到以下函数图象:
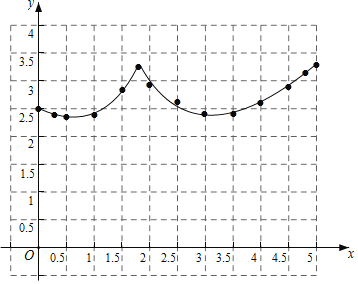
(3)当MN=BD时,即y=3,从图象看x即BM的长度大约是1.7,1.9,4.7;
故答案为:1.7,1.9,4.7(填的数值上下差0.1都算对).