Question

【题目】如图，在ABCD中，E是对角线BD上的一点，过点C作CF∥DB，且CF=DE，连接AE，BF，EF．

（1）求证：△ADE≌△BCF；

（2）若∠ABE+∠BFC=180°，则四边形ABFE是什么特殊四边形？说明理由．

Answer 1

【答案】（1）证明见解析；（2）四边形ABFE是菱形

【解析】

（1）根据平行四边形的性质和全等三角形的判定证明即可；
（2）根据平行四边形的性质和全等三角形的判定以及菱形的判定解答即可．

证明：（1）∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠ADB=∠DBC．

∵CF∥DB，∴∠BCF=∠DBC，∴∠ADB=∠BCF

在△ADE与△BCF中

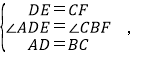∴△ADE≌△BCF（SAS）．

（2）四边形ABFE是菱形

理由：∵CF∥DB，且CF=DE，∴四边形CFED是平行四边形，∴CD=EF，CD∥EF．

∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴AB=EF，AB∥EF，∴四边形ABFE是平行四边形．

∵△ADE≌△BCF，∴∠AED=∠BFC．

∵∠AED+∠AEB=180°，∴∠ABE=∠AEB，∴AB=AE，∴四边形ABFE是菱形．