Question

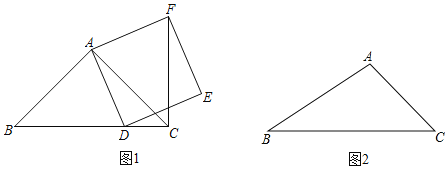
【题目】如图，在矩形ABMN中，AN=1，点C是MN的中点，分別连接AC，BC，且BC=2，点D为AC的中点，点E为边AB上一个动点，连接DE，点A关于直线DE的对称点为点F，分别连接DF，EF．当EF⊥AC时，AE的长为________．

Answer 1

【答案】或

【解析】

首先证明∠CAB=∠CBA=30°．分两种情形画出图形分别求解即可．

解：∵四边形ABMN是矩形，
∴AN=BM=1，∠M=∠N=90°，
∵CM=CN，
∴△BMC≌△ANC（SAS），
∴BC=AC=2，
∴AC=2AN，
∴∠ACN=30°，
∵AB∥MN，
∴∠CAB=∠CBA=30°，
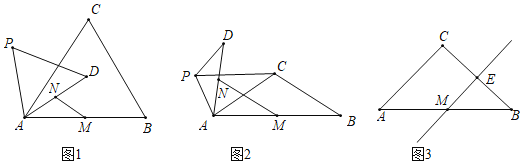
①如图1中，当DF⊥AB时，∠ADF=60°，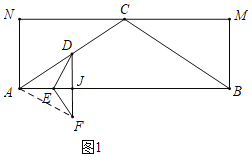

∵DA=DF，
∴△ADF是等边三角形，
∴∠AFD=60°，
∵∠DFE=∠DAE=30°，
∴EF平分∠AFD，
∴EF⊥AD，此时AE=．

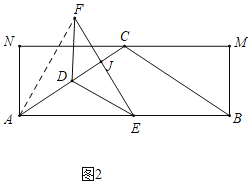
②如图2中，当△AEF是等边三角形时，EF⊥AC，此时EF=．

综上所述，满足条件的EF的值为或．