题目内容
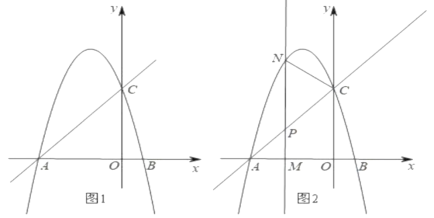
【题目】如图1，直线y=x+c与x轴交于点A(-3，0)，与y轴交于点C，抛物线y=-x2+bx+c经过点A、C．
（1）求抛物线的解析式；
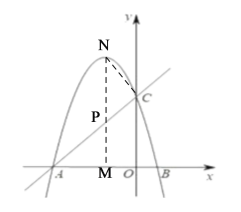
（2）如图2所示，M是线段0A上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N．若以C、P、N为顶点的三角形与△APM相似，求四边形MNCO的面积．
【答案】（1）y=-x2-2x+3；（2）6或
【解析】
（1）将A代入y=x+c求出c，从而求出C点坐标，再将A、C点代入y=-x2+bx+c算出解析式即可；
（2）△APM是直角三角形且
，根据C、P、N为顶点的三角形与△APM相似分为
或
进行分类讨论求出M、N点的坐标再求算四边形MNCO的面积即可．
解：（1）∵直线y=x+c与x轴交于点A(-3，0)，将A(-3，0)代入得：c=3
∴直线解析式为：y=x+3
∴C（0,3）
将A(-3，0)，C（0,3）代入y=-x2+bx+c得：
解得：
∴抛物线的解析式为：y=-x2-2x+3
（2）设
由题可知：
是直角三角形且，要使C、P、N为顶点的三角形与△APM相似
①当，如图：
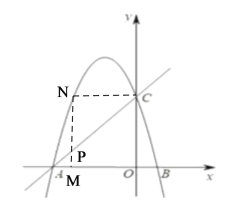
此时C、N在一条直线上
∴
∴四边形MNCO的面积=
②时，如图：
得出：
解得：
∴
∴四边形MNCO的面积=
综上所述：若以C、P、N为顶点的三角形与△APM相，四边形MNCO的面积为6或．
练习册系列答案
相关题目
