题目内容
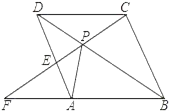
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)图中△APD与哪个三角形全等:_____.
(2)猜想:线段PC、PE、PF之间存在什么关系:_____.
【答案】(1)△APD≌△CPD(SAS);(2) PC2=PEPF.
【解析】
(1)根据菱形的性质得∠ADP=∠CDP,DA=DC,从而得到△APD与△CPD全等.
(2)根据菱形的对边互相平行得∠DCF=∠F,再根据(1)题的结论得到∠DCP=∠DAP,从而证得△PAE∽△PFA,然后利用比例线段证得等积式即可.
(1)∵四边形ABCD为菱形,
∴∠ADP=∠CDP,DC=DA,
在△APD和△CPD中,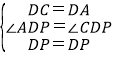 ,
,
∴△APD≌△CPD(SAS);
(2)∵四边形ABCD为菱形,
∴∠DCF=∠F,
∵△APD≌△CPD,
∴∠DCP=∠DAP,
∴∠F=∠PAE,
∠APE=∠FPA
∴△PAE∽△PFA,
∴![]() ,
,
即:PA2=PEPF,
∵P是菱形ABCD的对角线BD上一点,
∴PA=PC,
∴PC2=PEPF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目